
【题目】如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ). (Ⅰ)求
). (Ⅰ)求 ![]() ,
, ![]() 夹角的余弦值;
夹角的余弦值;
(Ⅱ)已知C(1,0),记∠AOC=α,∠BOC=β,求tan ![]() 的值.
的值.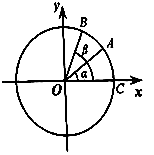
【答案】解:(Ⅰ)在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点 A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),
),
∴ ![]() =(
=( ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ),|
),| ![]() |=|
|=| ![]() |=1,
|=1,
∴ ![]() ,
, ![]() 夹角的余弦值cos∠AOB=
夹角的余弦值cos∠AOB=  =
=  =
= ![]() .
.
(Ⅱ)设∠AOB的平分线OD交单位圆于点D,则∠COD= ![]() ,
,
从而D(cos ![]() ,sin
,sin ![]() ),∴
),∴ ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
),
连接AB,可知OD⊥AB,即 ![]() =0.
=0.
∴ ![]() =
= ![]() ﹣
﹣ ![]() =(﹣
=(﹣ ![]() ,
, ![]() ),
),
∴(cos ![]() ,sin
,sin ![]() )(﹣
)(﹣ ![]() ,
, ![]() )=﹣
)=﹣ ![]() cos
cos ![]() +
+ ![]() sin
sin ![]() =0,
=0,
∴tan ![]() =
= ![]() .
.
【解析】(Ⅰ)先求出向量 ![]() ,
, ![]() 的坐标,再跟它们的夹角的余弦值cos∠AOB=
的坐标,再跟它们的夹角的余弦值cos∠AOB=  ,计算求得结果.(Ⅱ)设∠AOB的平分线OD交单位圆于点D,则∠COD=
,计算求得结果.(Ⅱ)设∠AOB的平分线OD交单位圆于点D,则∠COD= ![]() ,求得
,求得 ![]() 的坐标,根据
的坐标,根据 ![]() =0,求得tan
=0,求得tan ![]() 的值.
的值.
【考点精析】掌握数量积表示两个向量的夹角和两角和与差的正切公式是解答本题的根本,需要知道设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则;两角和与差的正切公式:
的夹角,则;两角和与差的正切公式:![]() .
.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的极值;
的极值;
(Ⅱ)设函数![]() .当
.当![]() 时,若区间
时,若区间![]() 上存在
上存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点. 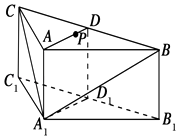
(1)在平面ABC内,试作出过点P与平面A1BC平行的直线l,并说明理由;
(2)证明:直线l⊥平面ADD1A1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)当 ![]() 时,求函数f(x)的取值范围;
时,求函数f(x)的取值范围;
(2)将f(x)的图象向左平移 ![]() 个单位得到函数g(x)的图象,求g(x)的单调递增区间.
个单位得到函数g(x)的图象,求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,锐角△ABC中, ![]() =
= ![]() ,
, ![]() =
= ![]() ,点M为BC的中点. (Ⅰ)试用
,点M为BC的中点. (Ⅰ)试用 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(Ⅱ)若| ![]() |=5,|
|=5,| ![]() |=3,sin∠BAC=
|=3,sin∠BAC= ![]() ,求中线AM的长.
,求中线AM的长.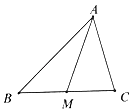
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内有4个不同的红球,6个不同的白球,
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a2x2+ax(a∈R).
(1)当a=1时,求函数f(x)最大值;
(2)若函数f(x)在区间(1,+∞)上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
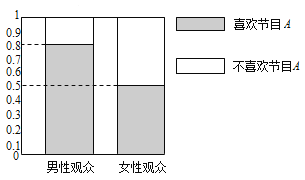
(1)根据该等高条形图,完成下列![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?

(2)从性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
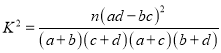 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,底面
中,底面![]() 是边长为 2 的正三角形,顶点
是边长为 2 的正三角形,顶点 ![]() 在底面
在底面![]() 上的射影为
上的射影为![]() 的中心,若
的中心,若![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() ,则三棱锥
,则三棱锥![]() 外接球的表面积为( )
外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com