
| A��1�� | B��2�� | C��3�� | D��4�� |


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
| a1(1-qn) |
| 1-q |
| a |
| cosA |
| b |
| cosB |
| c |
| cosC |
| x2+4 |
| 1 | ||
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��1�� | B��2�� | C��3�� | D��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
|
| a |
| b |
| A���٢ۢ� | B���٢ڢ� | C���٢ڢ� | D���ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
| 1 |
| 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A����x=1���ǡ�x2-3x+2=0���ij�ֲ���Ҫ���� |
| B����������p��?x��R��ʹ��x2+x+1��0����?p��?x��R������x2+x+1��0 |
| C�����⡰��m��0����x2+x-m=0��ʵ�������������Ϊ��������x2+x-m=0��ʵ������m��0�� |
| D�����⡰��xy=0����x��y��������һ��Ϊ�㡱�ķ�ʽ����xy��0����x��y����Ϊ�㡱 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A����f��0��=0���ǡ�����f��x�����溯�����ij�Ҫ���� | ||||||||
| B����p��?x0��R��x02-x0-1��0����Vp��?x��R��x2-x-1��0 | ||||||||
| C����p��qΪ�����⣬��p��q��Ϊ������ | ||||||||
D��������=
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A���٢� | B���٢� | C���ڢ� | D���ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
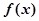
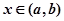 �ĵ�����Ϊ
�ĵ�����Ϊ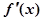 ��ԭ����Ϊ����
��ԭ����Ϊ����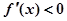 ����
����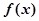 ��
��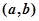 �ϵ����ݼ����������������⡢�����⡢�����������Ե��ж��������£���ȷ���ǣ� ��
�ϵ����ݼ����������������⡢�����⡢�����������Ե��ж��������£���ȷ���ǣ� ��| A���棬�棬�� | B���٣��٣��� |
| C���棬�棬�� | D���٣��٣��� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com