
【题目】已知函数![]()
![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在
在![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,求实数
,求实数![]() 与
与![]() 的值
的值
【答案】1解:(1)由已知条件得
![]() 对定义域中的
对定义域中的![]() 均成立.………………………………1分
均成立.………………………………1分
![]()
![]()
即![]()
![]()
![]() 对定义域中的
对定义域中的![]() 均成立.
均成立.
![]()
![]()
即![]() (舍去)或
(舍去)或![]() . …………………………………4分
. …………………………………4分
(2)由(1)得![]()
设![]() ,
,
![]() 当
当![]() 时,
时,![]()
![]()
![]() . ………………………………6分
. ………………………………6分
当![]() 时,
时,![]() ,即
,即![]() .
.
![]() 当
当![]() 时,
时,![]() 在
在![]() 上是减函数. ………………………………8分
上是减函数. ………………………………8分
同理当![]() 时,
时,![]() 在
在![]() 上是增函数. ………………………10分
上是增函数. ………………………10分
(3)![]() 函数
函数![]() 的定义域为
的定义域为![]() ,
,
![]() ①
①![]() ,
,![]()
![]() .
.
![]()
![]() 在
在![]() 为增函数,
为增函数,
要使值域为![]() ,
,
则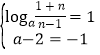 (无解)
(无解)
②![]() ,
,![]()
![]() .
.
![]()
![]() 在
在![]() 为减函数,
为减函数,
要使![]() 的值域为
的值域为![]() , 则
, 则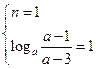
![]()
![]() ,
,![]() . ……………………………14分
. ……………………………14分
【解析】
试题
(1)由奇函数的性质得到关于实数m的方程,解方程可得m=-1;
(2)结合(1)的结论首先确定函数的解析式,结合对数函数的性质可知当a>1时,f(x)在(1,+∞)上单调递减; 当0<a<1时,f(x)在(1,+∞)上单调递增;
(3)结合奇函数的性质和(2)中确定的函数的单调性得到关于实数a,n的方程组,分类讨论求解方程组可得![]() .
.
试题解析:
(1)由![]() 为奇函数,则对定义域任意
为奇函数,则对定义域任意![]() 恒有
恒有![]() 即
即![]()
![]() (舍去1)
(舍去1)![]()
(2)由(1)得![]() ,当
,当![]() 时,
时,![]()
当![]() 时,
时,![]() 现证明如下:
现证明如下:
设![]() ,
,![]()
![]()
![]()
![]()
(3)由题意知![]() 定义域
定义域![]() 上的奇函数。
上的奇函数。
①当![]() 即
即![]() 时,由(2)知在(n,a-2)上f(x)为增函数,
时,由(2)知在(n,a-2)上f(x)为增函数,
由值域为(1,+∞)得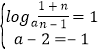 无解;
无解;
②当(n,a-2)(1,+∞)即1≤n<a-2有a/span>>3,
由(2)知在(n,a-2)上f(x)为减函数,
由值域为![]() 得
得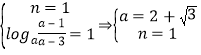


科目:高中数学 来源: 题型:
【题目】(1)抛掷一颗骰子两次,定义随机变量

试写出随机变量![]() 的分布列(用表格格式);
的分布列(用表格格式);
(2)抛掷一颗骰子两次,在第一次掷得向上一面点数是偶数的条件下,求第二次掷得向上一面点数也是偶数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系中,圆C的方程为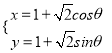 (θ为参数).以坐标原点O为极点,
(θ为参数).以坐标原点O为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程
的极坐标方程![]() .
.
(Ⅰ)当![]() 时,判断直线
时,判断直线![]() 与
与![]() 的关系;
的关系;
(Ⅱ)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的质量(单位:克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/克 | 频数 |
(490,495] | 6 |
(495,500] | 8 |
(500,505] | 14 |
(505,510] | 8 |
(510,515] | 4 |
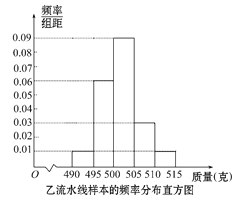
甲流水线样本频数分布表:
甲流水线 | 乙流水线 | 总计 | |
合格品 |
|
| |
不合格品 |
|
| |
总计 |
|
(1)根据上表数据作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从乙流水线任取![]() 件产品,该产品恰好是合格品的概率;
件产品,该产品恰好是合格品的概率;
(3)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为产品的包装质量与两条自动包装流水线的选择有关?
的前提下认为产品的包装质量与两条自动包装流水线的选择有关?
附表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: 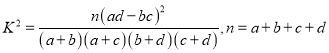 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x2-11x+18<0},B={x|-2≤x≤5}.
(1)求A∩B;B∪(UA);
(2)已知集合C={x|a≤x≤a+2},若C∩![]() =C,求实数a的取值范围.
=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的上、下焦点分别为F1 , F2 , 点D在椭圆上,DF2⊥F1F2 , △F1F2D的面积为2
=1(a>b>0)的上、下焦点分别为F1 , F2 , 点D在椭圆上,DF2⊥F1F2 , △F1F2D的面积为2 ![]() ,离心率e=
,离心率e= ![]() ,抛物线C:x2=2py(p>0)的准线l经过D点.
,抛物线C:x2=2py(p>0)的准线l经过D点.
(1)求椭圆E与抛物线C的方程;
(2)过直线l上的动点P作抛物线的两条切线,切点为A,B,直线AB交椭圆于M,N两点,当坐标原点O落在以MN为直径的圆外时,求点P的横坐标t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则取它的项:第一次取1;第二次取2个连续偶数2,4;第三次取3个连续奇数5,7,9;第四次取4个连续偶数10,12,14,16;第五次取5个连续奇数17,19,21,23,25,按此规律取下去,得到一个子数列1,2,4,5,7,9,10,12,14,16,17,19…,则在这个子数中第2014个数是( )
A. 3965 B. 3966 C. 3968 D. 3989
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣x2﹣ax.
(1)若曲线y=f(x)在点x=0处的切线斜率为1,求函数f(x)在[0,1]上的最值;
(2)令g(x)=f(x)+ ![]() (x2﹣a2),若x≥0时,g(x)≥0恒成立,求实数a的取值范围;
(x2﹣a2),若x≥0时,g(x)≥0恒成立,求实数a的取值范围;
(3)当a=0且x>0时,证明f(x)﹣ex≥xlnx﹣x2﹣x+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com