
【题目】已知函数![]()
(Ⅰ)若![]() 的图像与直线
的图像与直线![]() 相切,求
相切,求![]()
(Ⅱ)若![]() 且函数
且函数![]() 的零点为
的零点为![]() ,
,
设函数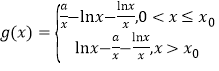 试讨论函数
试讨论函数![]() 的零点个数.(
的零点个数.(![]() 为自然常数)
为自然常数)
科目:高中数学 来源: 题型:
【题目】如图1,在△![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点, ![]() ,
,![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,如图2.
的中点,如图2.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求F到平面A1OB的距离.

图1 图2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图像与
的图像与![]() 的图像有交点,求
的图像有交点,求![]() 的取值范围;
的取值范围;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 最小值为1,若存在,求出
最小值为1,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆C过点
中,椭圆C过点![]() ,焦点
,焦点![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点,求点P的坐标;
②直线l与椭圆C交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列.在我国南宋数学家杨辉所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律.现把杨辉三角中的数从上到下,从左到右依次排列,得数列:![]() .记作数列
.记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ___ .
___ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上在第二象限内的一点,且直线
上在第二象限内的一点,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求![]() 点的坐标;
点的坐标;
(2)过点![]() 作一条斜率为正数的直线
作一条斜率为正数的直线![]() 与椭圆
与椭圆![]() 从左向右依次交于
从左向右依次交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
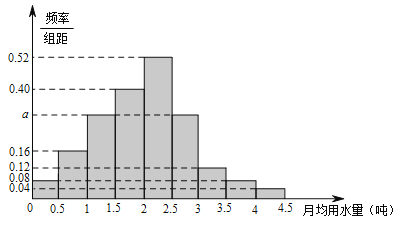
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com