
【题目】已知函数 ![]() ,直线l:x﹣ty﹣2=0.
,直线l:x﹣ty﹣2=0.
(1)若直线l与曲线y=f(x)有且仅有一个公共点,求公共点横坐标的值;
(2)若0<m<n,m+n≤2,求证:f(m)>f(n).
【答案】
(1)解:由 ![]() ,得f′(x)=
,得f′(x)= ![]() (x>0),
(x>0),
当x∈(0,1)时,f'(x)<0,f(x)单调递减,x∈(1,+∞)时,f'(x)>0,f(x)单调递增,
根据直线l的方程x=ty+2,可得l恒过点(2,0),
①当t=0时,直线l:x=2垂直x轴,与曲线y=f(x)相交于一点,即交点横坐标为2;
②当t≠0时,设切点A(x0,y0),直线l可化为 ![]() ,斜率k=
,斜率k= ![]() =f′(x0)=
=f′(x0)=  ,
,
又直线l和曲线y=f(x)均过点A(x0,y0),则满足 ![]() ,
,
∴  =
= 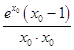 =
= ![]() =
= ![]() =
= ![]() ,两边约去t后,
,两边约去t后,
可得 ![]() ,化简得
,化简得 ![]() ,
,
解得: ![]() ,
,
综上所述,该公共点的横坐标为2和 ![]() ;
;
(2)证明:①若0<m<n≤1时,由(1)可知,f(x)在(0,1)上单调递减,
∴f(m)>f(n);
②若0<m<1,n>1时,欲证f(m)>f(n),由题意m+n≤2,由(1)可知f(x)在(1,+∞)上单调递减,
只需证f(m)>f(2﹣m)对m∈(0,1)恒成立即可.
设函数φ(m)=f(m)﹣f(2﹣m),则 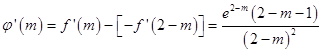 ,
,
即 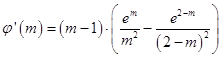 ,
,
设 ![]() ,则
,则 ![]() ,
,
易知x∈(0,2)时,h'(x)<0,h(x)单调递减,x∈(2,+∞)时,h'(x)>0,h(x)单调递增,
当m∈(0,1)时,有2﹣m∈(1,2),且满足2﹣m>m,故h(m)﹣h(2﹣m)>0,
即 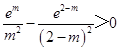 ,又m﹣1<0,则φ'(m)<0,
,又m﹣1<0,则φ'(m)<0,
∴φ(m)在(0,1)上单调递减,有φ(m)>φ(1)=0,
即f(m)>f(2﹣m),故f(m)>f(n).
综上,f(m)>f(n).
【解析】(1)求出原函数的导函数,得到函数的单调区间,由直线方程可知直线过定点,然后分t=0和t≠0分类求解A的横坐标;(2)若0<m<n≤1时,由(1)可知,f(x)在(0,1)上单调递减,可得f(m)>f(n);若0<m<1,n>1,把证明f(m)>f(n)转化为证f(m)>f(2﹣m)对m∈(0,1)恒成立即可.构造函数φ(m)=f(m)﹣f(2﹣m),利用两次求导加以证明.
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥平面BB1C1C,∠BCC1= ![]() ,AB=BB1=2,BC=1,D为CC1中点.
,AB=BB1=2,BC=1,D为CC1中点. 
(1)求证:DB1⊥平面ABD;
(2)求二面角A﹣B1D﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中其中真命题个数是( ) ①为了了解800名学生的成绩,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40;
②线性回归直线 ![]() =
= ![]() x+
x+ ![]() 恒过样本点的中心(
恒过样本点的中心( ![]() ,
, ![]() );
);
③随机变量ξ服从正态分布N(2,σ2)(σ>0),若在(﹣∞,1)内取值的概率为0.1,则在(2,3)内的概率为0.4;
④若事件M和N满足关系P(M∪N)=P(M)+P(N),则事件M和N互斥.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣k)ex+k,k∈Z,e=2.71828…为自然对数的底数.
(1)当k=0时,求函数f(x)的单调区间;
(2)若当x∈(0,+∞)时,不等式f(x)+5>0恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,动点P在其表面上运动,且|PA|=x,把点的轨迹长度L=f(x)称为“喇叭花”函数,给出下列结论: ① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]()
其中正确的结论是: . (填上你认为所有正确的结论序号)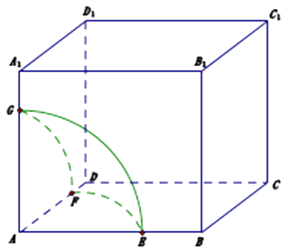
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点. 
(1)求证:FD∥平面ABC;
(2)求二面角B﹣FC﹣G的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若向量 ![]() ,在函数
,在函数 ![]() 的图象中,对称中心到对称轴的最小距离为
的图象中,对称中心到对称轴的最小距离为 ![]() ,且当
,且当 ![]() 的最大值为1.
的最大值为1.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】变量x,y满足约束条件  ,若使z=ax+y取得最大值的最优解有无穷多个,则实数a的取值集合是( )
,若使z=ax+y取得最大值的最优解有无穷多个,则实数a的取值集合是( )
A.{﹣3,0}
B.{3,﹣1}
C.{0,1}
D.{﹣3,0,1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com