
【题目】已知椭圆![]() ,过点
,过点![]() 的两条不同的直线与椭圆E分别相交于A,B和C,D四点,其中A为椭圆E的右顶点.
的两条不同的直线与椭圆E分别相交于A,B和C,D四点,其中A为椭圆E的右顶点.
(1)求以AB为直径的圆的方程;
(2)设以AB为直径的圆和以CD为直径的圆相交于M,N两点,探究直线MN是否经过定点,若经过定点,求出定点坐标;若不经过定点,请说明理由.
【答案】(1)![]() ;(2)经过定点,
;(2)经过定点,![]() .
.
【解析】
(1)由已知得AB方程:![]() ,与椭圆方程联立可求出
,与椭圆方程联立可求出![]() ,则可求出以AB为直径的圆的圆心和半径,进而可求出圆的方程;
,则可求出以AB为直径的圆的圆心和半径,进而可求出圆的方程;
(2)当CD斜率存在时,并设CD方程:![]() ,与椭圆方程联立,通过根与系数的关系可得以CD为直径的圆方程,将其与以AB为直径的圆的方程作差,可得直线MN的方程,进而可得直线MN过的定点
,与椭圆方程联立,通过根与系数的关系可得以CD为直径的圆方程,将其与以AB为直径的圆的方程作差,可得直线MN的方程,进而可得直线MN过的定点![]() ,当CD斜率不存在时,直线MN也过的定点
,当CD斜率不存在时,直线MN也过的定点![]() ,进而可得答案.
,进而可得答案.
(1)由已知![]() ,则
,则![]() ,故AB方程:
,故AB方程:![]() ,
,
联立直线AB与椭圆方程,消去y可得:![]() ,得
,得![]() ,即
,即![]() ,
,
从而以AB为直径的圆的圆心为![]() ,半径为
,半径为 ,
,
所以圆的方程为 ,
,
即![]() .;
.;
(2)①当CD斜率存在时,并设CD方程:![]() ,
,
设![]() ,
,![]()
由 ,消去y得:
,消去y得:![]() ,
,
故![]() ,
,![]() ,
,
从而![]() ,
,
![]() ,
,
而以CD为直径的圆方程为:![]() ,
,
即![]() ①,
①,
且以AB为直径的圆方程为![]() ②,
②,
②-①得直线![]() ,
,
即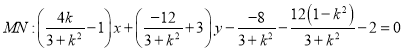
整理得![]() ,
,
可得:![]() ,
,
因为AB与 CD两条直线互异,则![]() ,
,
即![]() ,
,
令![]() ,解得
,解得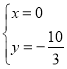 ,即直线MN过定点
,即直线MN过定点![]() ;
;
②当CD斜率不存在时,CD方程:![]() ,知
,知![]() ,
,![]() ,
,
则以CD为直径的圆为![]() ,
,
而以AB为直径的圆方程![]() ,
,
两式相减得MN方程:![]() ,过点
,过点![]() ;
;
综上所述,直线MN过定点![]() .
.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为椭圆的左右焦点,点
分别为椭圆的左右焦点,点![]() 为椭圆
为椭圆![]() 上的一动点,
上的一动点,![]() 面积的最大值为2.
面积的最大值为2.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,点
,点![]() ,证明:直线
,证明:直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC三个内角A,B,C所对的边,且![]() .
.
(1)求B;
(2)若b=2,且sinA,sinB,sinC成等差数列,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: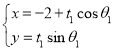 (
(![]() 为参数),曲线
为参数),曲线![]() :
: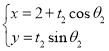 (
(![]() 为参数),且
为参数),且![]() ,点P为曲线
,点P为曲线![]() 与
与![]() 的公共点.
的公共点.
(1)求动点P的轨迹方程;
(2)在以原点O为极点,x轴的非负半轴为极轴的极坐标系中,直线l的极坐标方程为![]() ,求动点P到直线l的距离的取值范围.
,求动点P到直线l的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,是奇函数.
,是奇函数.
(1)求实数m的值;
(2)画出函数![]() 的图象,并根据图象求解下列问题;
的图象,并根据图象求解下列问题;
①写出函数![]() 的值域;
的值域;
②若函数![]() 在区间
在区间![]() 上单调递增,求实数a的取值范围.
上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】作家马伯庸小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行,每一列上至多有一个紫色小方格(如图所示即满足要求).则一共可以传递______种信息.(用数字作答)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:![]() ,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),设原点
为参数),设原点![]() 在圆
在圆![]() 的内部,直线
的内部,直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点;以坐标原点
两点;以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程,并求
的极坐标方程,并求![]() 的取值范围;
的取值范围;
(2)求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com