
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知c=acosB+bsinA.
(1)求A;
(2)若a=2,b=c,求△ABC的面积.
【答案】
(1)解:由c=acosB+bsinA及正弦定理可得:sinC=sinAcosB+sinBsinA.…(2分)
在△ABC中,C=π﹣A﹣B,
所以sinC=sin(A+B)=sinAcosB+cosAsinB.
由以上两式得sinA=cosA,即tanA=1,
又A∈(0,π),
所以A= ![]()
(2)解:由于S△ABC= ![]() bcsinA=
bcsinA= ![]() bc,
bc,
由a=2,及余弦定理得:4=b2+c2﹣2bccosB=b2+c2﹣ ![]() ,
,
因为b=c,
所以4=2b2﹣ ![]() b2,即b2=
b2,即b2= ![]() =4
=4 ![]()
故△ABC的面积S= ![]() bc=
bc= ![]() b2=
b2= ![]()
【解析】(1)由已知及正弦定理,三角形内角和定理,两角和的正弦函数公式,同角三角函数基本关系式可得:tanA=1,结合范围A∈(0,π),可求A的值.(2)由三角形面积公式及余弦定理可求b2的值,进而利用三角形面积公式即可计算得解.


科目:高中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,已知A(﹣2,0),直角顶点B(0,﹣2 ![]() ),点C在x轴上. (Ⅰ)求Rt△ABC外接圆的方程;
),点C在x轴上. (Ⅰ)求Rt△ABC外接圆的方程;
(Ⅱ)求过点(﹣4,0)且与Rt△ABC外接圆相切的直线的方程.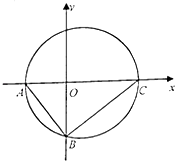
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x﹣5|.
(1)当a=1时,求f(x)的最小值;
(2)如果对任意的实数x,都有f(x)≥1成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(﹣x)=8﹣f(4+x),函数g(x)= ![]() ,若函数f(x)与g(x)的图象共有168个交点,记作Pi(xi , yi)(i=1,2,…,168),则(x1+y1)+(x2+y2)+…+(x168+y168)的值为( )
,若函数f(x)与g(x)的图象共有168个交点,记作Pi(xi , yi)(i=1,2,…,168),则(x1+y1)+(x2+y2)+…+(x168+y168)的值为( )
A.2018
B.2017
C.2016
D.1008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力部门需在A、B两地之间架设高压电线,因地理条件限制,不能直接测量A、B两地距离.现测量人员在相距 ![]() km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的
km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的 ![]() 倍,问施工单位应该准备多长的电线?
倍,问施工单位应该准备多长的电线? 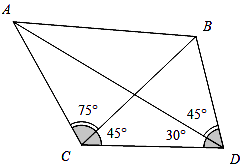
查看答案和解析>>
科目:高中数学 来源: 题型:
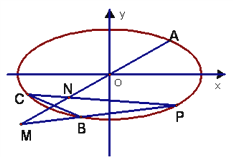
【题目】如图,在平面直角坐标系中,已知A、B、C是椭圆![]() 上不同的三点,
上不同的三点,  ,C在第三象限,线段BC的中点在直线OA上。
,C在第三象限,线段BC的中点在直线OA上。
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点P在椭圆上(异于点A、B、C)且直线PB, PC分别交直线OA于M、N两点,证明![]() 为定值并求出该定值.
为定值并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苏州市一木地板厂生产A、B、C三类木地板,每类木地板均有环保型和普通两种型号,某月的产量如下表(单位:片):
类型 | 木地板A | 木地板B | 木地板C |
环保型 | 150 | 200 | Z |
普通型 | 250 | 400 | 600 |
按分层抽样的方法在这个月生产的木地板中抽取50片,其中A类木地板10片.
(1)求Z的值;
(2)用随机抽样的方法从B类环保木地板抽取8片,作为一个样本,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,从中任取一个数,求该数与样本平均数之差的绝对不超过0.5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com