
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() ,且
,且![]() ,则
,则![]() __________.
__________.

【答案】-4
【解析】分析:先利用同角三角的基本关系求得sinC和sin∠DBC的值,结合∠BDA=C+∠DBC,利用两角和的余弦公式求得 cos∠BDA 的值,可得∠BDA 的值.
再求出△ABC中各边的长,再由D是AC上一点,![]() ,我们将相关数据代入平面向量数量积公式即可求解.
,我们将相关数据代入平面向量数量积公式即可求解.
详解:△ABC中,∵cosC=![]() ,cos∠DBC=
,cos∠DBC=![]() ,
,
∴sinC=![]() ,sin∠DBC=
,sin∠DBC=![]() ,
,
∵∠BDC=π﹣C﹣∠DBC,
∴∠BDA=C+∠DBC,
∴cos∠BDA=cos(C+∠DBC )=cosCcos∠DBC﹣sinCsin∠DBC
=![]() ×
×![]() ﹣
﹣![]() =
=![]() ,
,
∴∠BDA=![]() .
.
设DC=x,BC=a,
在△BDC中,由正弦定理得![]() ,
,
∴a= ,
,
在△ABC中,AC=3x,BC=![]() ,AB=2,
,AB=2,
∴cosC=![]() =
=![]() ,解得x=1,∴AD=2,CB=
,解得x=1,∴AD=2,CB=![]() ,
,
∴![]() =2
=2![]() cos(π﹣C)=2
cos(π﹣C)=2![]() (﹣cosC)=﹣2
(﹣cosC)=﹣2![]()
![]() =﹣4.
=﹣4.
故填-4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,并且满足
,并且满足![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() ;
;
(3)在(2)的条件下,是否存在常数![]() ,使得数列
,使得数列![]() 为等比数列?若存在,试求出
为等比数列?若存在,试求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
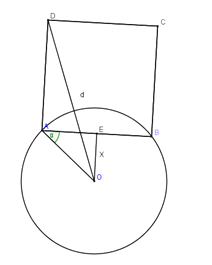
【题目】某飞机失联,经卫星侦查,其最后出现在小岛![]() 附近,现派出四艘搜救船
附近,现派出四艘搜救船![]() ,为方便联络,船
,为方便联络,船![]() 始终在以小岛
始终在以小岛![]() 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船![]() 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛![]() 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() ,
,![]() 船到小岛
船到小岛![]() 的距离为
的距离为![]() .
.
(1)请分别求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并分别写出定义域;
,并分别写出定义域;
(2)当![]() 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即![]() 最大)?
最大)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用 ![]() 表示.
表示.
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求 ![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t ≠ 0),其中0 ≤ α < π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
(t为参数,t ≠ 0),其中0 ≤ α < π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2: ![]() ,C3:
,C3: ![]() .
.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是 ![]() 或
或 ![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() ,
, ![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是 ![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数为( )
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”;
②“x≠3”是“|x|≠3”成立的充分条件;
③命题“若m≤ ![]() ,则方程mx2+2x+2=0有实数根”的否命题为真命题.
,则方程mx2+2x+2=0有实数根”的否命题为真命题.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f (x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com