
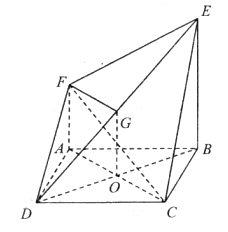
【题目】如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.

(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求证:AC∥平面DEF;
(Ⅲ)求三棱锥A—DEF的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ) ![]() .
.
【解析】试题分析:
(Ⅰ)由面面垂直的性质可得BE⊥平面ABCD,BE⊥AC,且AC⊥BD.结合线面垂直的判断定理有AC⊥平面BDE.
(Ⅱ)设AC∩BD=O,很明显O为BD中点,设G为DE的中点,连结OG,FG,结合几何关系可证得四边形AOGF为平行四边形,故AC∥FG,由线面平行的判断定理可得AC∥平面DEF.
(Ⅲ)由(Ⅰ)可知BE⊥平面ABCD,则AF⊥AD.又AB⊥AD,故AD⊥平面ABEF,转化顶点有: ![]() .
.
试题解析:
(Ⅰ)因为平面ABCD⊥平面ABEF,
平面ABCD∩平面ABEF=AB,且AB⊥BE,所以BE⊥平面ABCD,
因为![]() 平面ABCD,所以BE⊥AC,
平面ABCD,所以BE⊥AC,
又因为四边形ABCD为正方形,所以AC⊥BD.
因为BD∩BE=B,所以AC⊥平面BDE.
(Ⅱ)设AC∩BD=O,
因为四边形ABCD为正方形,
所以O为BD中点,
设G为DE的中点,连结OG,FG,
则OG∥BE,且![]() ,
,
由已知AF∥BE,且![]() ,
,
则AF∥OG,且AF=OG.
所以四边形AOGF为平行四边形,
所以AO∥FG,即AC∥FG,
因为![]() 平面DEF,
平面DEF, ![]() 平面DEF,
平面DEF,
所以AC∥平面DEF.
(Ⅲ)由(Ⅰ)可知BE⊥平面ABCD,
因为AF∥BE,所以AF⊥平面ABCD,
所以AF⊥AB,AF⊥AD.
又因为四边形ABCD为正方形,所以AB⊥AD,
所以AD⊥平面ABEF,
因为AB=AD=2AF=2,
所以![]()
![]() ,
,
故三棱锥![]() 的体积为
的体积为![]() .
.


 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,且x=-1处取得极大 值2.
为奇函数,且x=-1处取得极大 值2.
(1)求f(x)的解析式;
(2)过点A(1,t) ![]() 可作函数f(x)图像的三条切线,求实数t的取值范围;
可作函数f(x)图像的三条切线,求实数t的取值范围;
(3)若![]() 对于任意的
对于任意的![]() 恒成立,求实数m取值范围.
恒成立,求实数m取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的长轴长为4,焦距为
的长轴长为4,焦距为![]() .
.
(Ⅰ)求椭圆C的方程;

(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点,过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、![]() ,证明
,证明![]() 为定值.
为定值.
(ii)求直线AB的斜率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是偶函数,定义x≥0时,f(x)=![]()
(1)求f(-2);
(2)当x<-3时,求f(x)的解析式;
(3)设函数y=f(x)在区间[-5,5]上的最大值为g(a),试求g(a)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级某次数学竞赛随机抽取100名学生的成绩,分组为[50,60),[60,70),[70,80),[80,90),[90,100],统计后得到频率分布直方图如图所示:

(1)试估计这组样本数据的众数和中位数(结果精确到0.1);
(2)年级决定在成绩[70,100]中用分层抽样抽取6人组成一个调研小组,对高一年级学生课外学习数学的情况做一个调查,则在[70,80),[80,90),[90,100]这三组分别抽取了多少人?
(3)现在要从(2)中抽取的6人中选出正副2个小组长,求成绩在[80,90)中至少有1人当选为正、副小组长的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com