
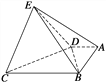
【题目】在如图所示的几何体中,底面ABCD中,AB⊥AD,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
(1)求证:平面DEC⊥平面BDE;
(2)求点A到平面BDE的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由勾股定理及逆定理可得![]() ,从而有线面垂直,于是可得面面垂直;
,从而有线面垂直,于是可得面面垂直;
(2)![]() 到平面
到平面![]() 的距离可用体积法求得,
的距离可用体积法求得, ![]() .
.
试题解析:
(1)证明 因为AB⊥AD,AD=2,AB=3,所以BD=![]() ,
,
又因为BC=7,CD=6,所以根据勾股定理可得BD⊥CD,
因为BE=7,DE=6,同理可得BD⊥DE.
因为DE∩CD=D,DE平面DEC,CD平面DEC,
所以BD⊥平面DEC.因为BD平面BDE,
所以平面DEC⊥平面BDE.

(2)解 如图,取CD的中点O,连接OE,
因为△DCE是边长为6的正三角形,
所以EO⊥CD,EO=3![]() ,
,
易知EO⊥平面ABCD,
则VE-ABD=![]() ×
×![]() ×2×3×3
×2×3×3![]() =3
=3![]() ,
,
又因为直角三角形BDE的面积为![]() ×6×
×6×![]() =3
=3![]() ,
,
设点A到平面BDE的距离为h,则由VE-ABD=VA-BDE,
得![]() ×3
×3![]() h=3
h=3![]() ,所以h=
,所以h=![]() ,所以点A到平面BDE的距离为
,所以点A到平面BDE的距离为![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() (e=2.71828
(e=2.71828![]() ,是自然对数的底数)在
,是自然对数的底数)在![]() 的定义域上单调递增,则称函数
的定义域上单调递增,则称函数![]() 具有M性质,下列函数中具有M性质的是( )
具有M性质,下列函数中具有M性质的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 为抛物线
为抛物线![]() 上不同的两点,
上不同的两点, ![]() 分别是抛物线
分别是抛物线![]() 在点
在点![]() 、点
、点![]() 处的切线,
处的切线, ![]() 是
是![]() 的交点.
的交点.
(1)当直线![]() 经过焦点
经过焦点![]() 时,求证:点
时,求证:点![]() 在定直线上;
在定直线上;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,且
内单调递增,且![]() 在
在![]() 上有三个零点,1是其中一个零点.
上有三个零点,1是其中一个零点.
(1)求![]() 的取值范围;
的取值范围;
(2)若直线![]() 在曲线
在曲线![]() 的上方部分所对应的
的上方部分所对应的![]() 的集合为
的集合为![]() ,试求实数
,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:

(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:

(1)求高三(1)班全体女生的人数;
(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)之间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析女生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() .
.
(1)求函数![]() 在
在![]() 上的单调区间,并给以证明;
上的单调区间,并给以证明;
(2)设关于![]() 的方程
的方程![]() 的两根为
的两根为![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意的
对任意的![]() 及
及![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com