
【题目】已知函数f(x)=![]() 为定义在R上的奇函数.
为定义在R上的奇函数.
(1)求a,b的值及f(x)的表达式;
(2)判断f(x)在定义域上的单调性并用单调性的定义证明.
【答案】(1)![]() (2)增函数
(2)增函数
【解析】
试题分析:(1)由函数为奇函数可知![]() 恒成立,由此带入可求得
恒成立,由此带入可求得![]() 值,进而得到函数解析式;
值,进而得到函数解析式;
(2)证明函数单调性一般采用定义法,首先假设![]() ,通过判断
,通过判断![]() 的大小关系证明函数单调性
的大小关系证明函数单调性
试题解析:(1)∵f(x)=![]() 定义在R上的奇函数,
定义在R上的奇函数,
则有f(0)=0,即![]() =0,解可得a=1;………………2分
=0,解可得a=1;………………2分
又f(1)=﹣f(﹣1),即![]() =﹣
=﹣![]() ,解可得b=1.……………4分
,解可得b=1.……………4分
∴f(x)=![]() ;………………5分
;………………5分
(2)由(1)可得,f(x)=1﹣![]() ………………6分
………………6分
设x1<x2,………………………………………………7分
则f(x1)﹣f(x2)=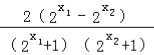 ,………………9分
,………………9分
∵x1<x2,
∴![]() <0,………………………………10分
<0,………………………………10分
∴f(x1)﹣f(x2)<0,………………11分
∴f(x)是增函数.………………12分


科目:高中数学 来源: 题型:
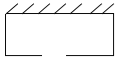
【题目】围建一个面积为![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2![]() 的进出口,如图所示,已知旧墙的维修费用为
的进出口,如图所示,已知旧墙的维修费用为![]() 元/
元/![]() ,新墙的造价为
,新墙的造价为![]() 元/
元/![]() ,设利用的旧墙的长度为
,设利用的旧墙的长度为![]() ,费用为
,费用为![]() 元.
元.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() 的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
(1)求(RA)∩B;
(2)若(A∪B)∩C≠,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
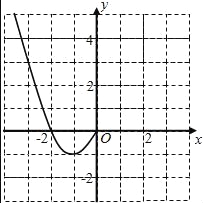
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①垂直于同一平面的两条直线相互平行;
②平行于同一平面的两条直线相互平行;
③若一条直线平行于一个平面内的无数条直线,那么这条直线平行于这个平面;
④若一条直线垂直于一个平面内的任一条直线,那么这条直线垂直于这个平面.
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计资料,我国能源生产自1992年以来发展很快,下面是我国能源生产总量(折合亿吨标准煤)的几个统计数据:1992年8.6亿吨,5年后的1997年10.4亿吨,10年后的2002年12.9亿吨.有关专家预测,到2007年我国能源生产总量将达到17.1亿吨,则专家是依据下列哪一类函数作为数学模型进行预测的( )
A.一次函数 B.二次函数 C.指数函数 D.对数函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)=loga(2+x)-loga(2-x)(a>0且a≠1)
(Ⅰ)求f(x)定义域;
(Ⅱ)判断f(x)的奇偶性,并说明理由;
(Ⅲ)求使f(x)>0的x的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是
A. 四边形确定一个平面
B. 经过一条直线和一个点确定一个平面
C. 经过三点确定一个平面
D. 两两相交且不共点的三条直线确定一个平面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com