练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．若（ax-l）6展开式中x3的系数为20，则a的值为-1．

    分析 在二项展开式的通项公式中，令x的幂指数等于3，求出r的值，即可求得展开式中x3的系数，再根据展开式中x3的系数为20，求得a的值．

    解答 解：（ax-l）6展开式的通项公式为 Tr+1=${C}_{6}^{r}$•（-1）r•a6-r•x6-r，令6-r=3，求得r=3，
    故展开式中x3的系数为-${C}_{6}^{3}$•a3=20，∴a=-1，
    故答案为：-1．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．实数x，y，z满足x＞0，y＞0，z＞0，求证：$\sqrt{x}+\sqrt{y}+\sqrt{z}≤\frac{x}{2}+\frac{y}{2}+\frac{z}{2}+\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．期中考试后，某教师对其所教的甲、乙两个班的学生试卷进行卷面分析．已知甲、乙两班成绩在80分以上的学生分别有20人和16人，现用分层抽样法从甲、乙两班成绩在80分以上的学生中抽取9人进行分析．
    （I）若从所抽取的9人中任选4人进行运算错误分析，求这4人不是同一个班的概率；
    （Ⅱ）若从所抽取的9人中任选3人进行题意理解错误分析，记这3人中乙班的人数为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．袋中装有大小相等，质地均匀的4个小球，其中有2个黑球和2个白球，游戏规则如下：甲每次从袋中任取一球，记录后放回，共取3次；乙一次性从袋中取3个球，并记录下颜色，甲、乙两人取球互不影响，求：
    （1）甲取球3次后记录所得的黑球次数大于乙所取黑球个数的概率；
    （2）设甲每次取到黑球得1分，取到白球得0分，游戏结束后甲所得总分为X，乙所得的总分为Y（取到1个黑球得1分，取到2个黑球得2分），记ξ=|X-Y|，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知集合A={x|-1≤x≤1），集合B={x|x2-2x≤0），则集合A∩B=（　　）
    A．[-1，0]B．[-1，2]C．[0，1]D．（一∞，1]∪[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

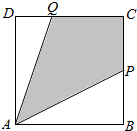    5．如图，有一块边长为1（百米）的正方形区域ABCD．在点A处有一个可转动的探照灯，其照射角∠PAQ始终为45°（其中点P，Q分别在边BC，CD上），设BP=t．
    （I）用t表示出PQ的长度，并探求△CPQ的周长l是否为定值；
    （Ⅱ）设探照灯照射在正方形ABCD内部区域的面积S（平方百米），求S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．表是某市从3月份中随机抽取的10天空气质量指数（AQI）和“PM2.5”（直径小于等于2.5微米的颗粒物）24小时平均浓度的数据，空气质量指数（AQI）小于100表示空气质量优良．
    日期编号A1A2A3A4A5A6A7A8A9A10
    空气质量指数（AQI）1794098124291332414249589
    PM2.5日均浓度（ug/m3）13558094801001903877066
    （1）根据表数据，估计该市当月某日空气质量优良的概率；
    （2）在表数据中、在表示空气质量优良的日期中，随机抽取两个对其当天的数据作进一步的分析，设事件M为“抽取的两个日期中，当天‘PM2.5’的24小时平均浓度小于75ug/m3”，求事件M发生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设f（x）是定义在R上的函数，满足f（x+2）=-f（x），且x∈[0，2]时，f（x）=2x-x2
    （1）求x∈[-2，0]时，f（x）的表达式；
    （2）求f（9）和f（-9）的值；
    （3）猜想：f（x）在R上的奇偶性（不必证明）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知数列{an}满足na1+（n-1）a2+…+2an-1+an=n2（n+1），数列{bn}满足：b1=2，且11bn+1-10bn-1=0．
    （I）证明：数列{bn-1}等比；
    （Ⅱ）求数列{an}的通项；
    （Ⅲ）若cn=$\frac{10}{11}$an•（bn-1），求cn最大时的n值．

    查看答案和解析>>

    同步练习册答案