练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)=-x+log2.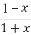

    (1)求f()+f(-)的值.

    (2)当x∈(-a,a],其中a∈(0,1),a是常数时,函数f(x)是否存在最小值?若存在,求出f(x)的最小值;若不存在,请说明理由.

     

    (1)0 (2) f(x)存在最小值,且为log2-a

    【解析】∵f(x)的定义域为(-1,1),关于原点对称,

    (1)f(-x)=x+log2=x-log2,

    ∴f(-x)=-f(x),故f(x)在(-1,1)上是奇函数,

    因此f()+f(-)=f()-f()=0.

    (2)∵f(x)=-x+log2(-1+),

    令U(x)=-1+,

    则U(x)在(-1,1)上是减函数,

    ∴f(x)在(-1,1)上是减函数.

    又a∈(0,1),∴当x∈(-a,a]时,f(x)是减函数,

    故f(x)min=f(a)=-a+log2,

    ∴f(x)存在最小值,且为log2-a.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷（解析版） 题型：解答题

    在极坐标系中，O为极点，半径为2的圆C的圆心的极坐标为.

    (1)求圆C的极坐标方程；

    (2)P是圆C上一动点，点Q满足3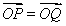，以极点O为原点，以极轴为x轴正半轴建立直角坐标系，求点Q的轨迹的直角坐标方程．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（四）第二章第一节练习卷（解析版） 题型：填空题

    已知f(x)=则f(f(1))的值等于　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（六）第二章第三节练习卷（解析版） 题型：填空题

    设函数f(x)=为奇函数,则实数a=　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（六）第二章第三节练习卷（解析版） 题型：选择题

    已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f(),b=f(),c=f(),则(　　)

    (A)c<a<b (B)a<b<c (C)b<a<c (D)c<b<a

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（八）第二章第五节练习卷（解析版） 题型：选择题

    设函数f(x)=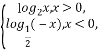若f(a)>f(-a),则实数a的取值范围是(　　)

    (A)(-1,0)∪(0,1)

    (B)(-∞,-1)∪(1,+∞)

    (C)(-1,0)∪(1,+∞)

    (D)(-∞,-1)∪(0,1)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（八）第二章第五节练习卷（解析版） 题型：选择题

    已知a=log23.6,b=log43.2,c=log43.6,则(　　)

    (A)a>b>c (B)a>c>b

    (C)b>a>c (D)c>a>b

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（五）第二章第二节练习卷（解析版） 题型：选择题

    给定函数①y=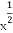,②y=lo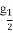(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上是单调递减的函数的序号是(　　)

    (A)①② (B)②③ (C)③④ (D)①④

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（三）第一章第三节练习卷（解析版） 题型：选择题

    下列四个命题

    p1:?x∈(0,+∞),()x<()x;

    p2:?x∈(0,1),lox>lox;

    p3:?x∈(0, +∞),()x>lox;

    p4:?x∈(0,),()x<lox.

    其中的真命题是(　　)

    (A)p1,p3 (B)p1,p4 (C)p2,p3 (D)p2,p4

     

    查看答案和解析>>

    同步练习册答案