
(本题12分)在人流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
(1)0.05;(2)0.45;(3)1200元
【解析】先列出所有基本事件:把3只黄色乒乓球标记为A、B、C,3只白色的乒乓球标记为1、2、3.从6个球中随机摸出3个的基本事件为:ABC、AB1、AB2、AB3、AC1、AC2、AC3、A12、A13、A23、BC1、BC2、BC3、B12、B13、B23、C12、C13、C23、123,共20个.
(1)(2)分别求出对应事件包括的基本事件的个数,然后利用古典概型概率计算公式计算即可.
(3)根据由摸出的3个球为同一颜色的概率估计出发生的次数,则可计算一天可赚多少钱.
解:把3只黄色乒乓球标记为A、B、C,3只白色的乒乓球标记为1、2、3.从6个球中随机摸出3个的基本事件为:ABC、AB1、AB2、AB3、AC1、AC2、AC3、A12、A13、A23、BC1、BC2、BC3、B12、B13、B23、C12、C13、C23、123,共20个………………(3分)
1)、设事件E={摸出的3个球为白球},事件E包含的基本事件有1个,即摸出123号3个球,所以 P(E)=1/20=0.05 ………………(5分)
2)、事件F={摸出的3个球为2个黄球1个白球},事件F包含的基本事件有9个,P(F)=9/20=0.45 ………………(8分)
3)、事件G={摸出的3个球为同一颜色}={摸出的3个球为白球或摸出的3个球为黄球},P(G)=2/20=0.1,假定一天中有100人次摸奖,由摸出的3个球为同一颜色的概率可估计事件G发生有10次,不发生90次.则一天可赚 ,每月可赚1200元.……(12分)
,每月可赚1200元.……(12分)


科目:高中数学 来源: 题型:
(本题12分)在数列{an}中,a1=2,an+1=4 an-3n+1,n∈N*.
(1)证明数列{an-n}是等比数列;(2)求数列{an}的前n项和Sn;(3)证明不等式Sn+1≤4Sn,对任意n∈N*皆成立。
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高二上学期期末理科数学试卷(解析版) 题型:解答题
(本题12分)在直角梯形PBCD中,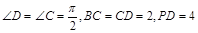 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将 沿AB折到
沿AB折到 的位置,使
的位置,使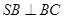 ,点E在SD上,且
,点E在SD上,且 ,如下图。
,如下图。
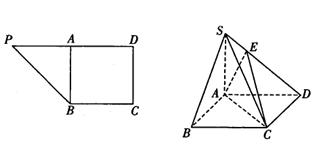
(1)求证: 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.
查看答案和解析>>
科目:高中数学 来源:2014届北京师大附中高一第二学期期中考试数学试卷(解析版) 题型:解答题
(本题12分)在 中,
中, ,
, ,
, 的对边分别为a,b,c。若a+c=20,
的对边分别为a,b,c。若a+c=20, ,
,
(1)求 的值; (2)求b的值。
的值; (2)求b的值。
查看答案和解析>>
科目:高中数学 来源:2013届安徽省高二3月月考文科数学试卷 题型:解答题
(本题12分)
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD, AP=AB, BP=BC=2,E,F分别是PB,PC的中点
(1) 证明:EF 面PAD
面PAD
(2) 求三棱锥E-ABC的体积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com