
【题目】已知函数f(x)=ax2+21nx.
(1)求f(x)的单调区间.
(2)若f(x)在(0,1]上的最大值是﹣2,求a的值.
(3)记g(x)=f(x)+(a﹣1)lnx+1,当a≤﹣2时,若对任意x1 , x2∈(0,+∞),总有|g(x1)﹣g(x2)|≥k|x1﹣x2|成立,试求k的最大值.
【答案】
(1)解:函数f(x)=ax2+21nx(x>0)的导数为f′(x)=2ax+ ![]() =
= ![]() ,
,
当a≥0时,f′(x)>0,f(x)递增;
当a<0时,f′(x)>0解得0<x< ![]() ;f′(x)<0解得x>
;f′(x)<0解得x> ![]() .
.
即有a≥0时,f(x)的增区间为(0,+∞);
a<0时,f(x)的增区间为(0, ![]() );减区间为(
);减区间为( ![]() ,+∞)
,+∞)
(2)解:由(1)可得a≥0时,f(x)在(0,1]递增,f(1)取得最大,且为a=﹣2,舍去;
a<0时,若1≤ ![]() 即﹣1≤a<0时,f(x)在(0,1]递增,
即﹣1≤a<0时,f(x)在(0,1]递增,
则f(1)=a取得最大值,且为a=﹣2<﹣1,不成立;
若1> ![]() 即a<﹣1时,f(x)在(0,
即a<﹣1时,f(x)在(0, ![]() )递增,(
)递增,( ![]() ,1]递减,.
,1]递减,.
则f( ![]() 取得最大值,且为﹣1+2ln
取得最大值,且为﹣1+2ln ![]() =﹣2,解得a=﹣e<﹣1,成立.
=﹣2,解得a=﹣e<﹣1,成立.
综上可得a=﹣e
(3)解:g(x)=f(x)+(a﹣1)lnx+1=ax2+(a+1)lnx+1,
g′(x)=2ax+ ![]() <0,(a≤﹣2),即有g(x)在(0,+∞)递减,
<0,(a≤﹣2),即有g(x)在(0,+∞)递减,
令x1<x2,则g(x1)>g(x2),
若对任意x1,x2∈(0,+∞),总有|g(x1)﹣g(x2)|≥k|x1﹣x2|成立,
即为g(x1)﹣g(x2)≥k(x2﹣x1),即g(x1)+kx1≥g(x2)+kx2,
则h(x)=g(x)+kx在(0,+∞)递减,
即有h′(x)=g′(x)+k≤0恒成立,
则﹣k≥2ax+ ![]() 的最大值,
的最大值,
由a≤﹣2,2ax+ ![]() ≤﹣4x﹣
≤﹣4x﹣ ![]() =﹣(4x+
=﹣(4x+ ![]() )≤﹣2
)≤﹣2 ![]() =﹣4,
=﹣4,
当且仅当x= ![]() 时,取得最大值﹣4,
时,取得最大值﹣4,
则﹣k≥﹣4,即k≤4,则k的最大值为4
【解析】(1)求出f(x)的导数,讨论a≥0时,a<0时,由导数大于0,可得增区间;导数小于0,可得减区间;(2)由(1)可得,可得a≥0时,f(x)在(0,1]递增,f(1)最大为﹣2,解方程可得;a<0时,求得极值点,与区间( ),1]的关系,可得最大值,解方程可得a的值;(3)求得g(x)的导数,判断符号可得单调性,再由条件可得h(x)=g(x)+kx递减,运用导数,结合基本不等式可得k的最大值.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的最大(小)值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知动点 P 与定点![]() 的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
(1)求曲线 E 的方程;
(2)设 A 是曲线 E 上的一个点,直线 AF 交曲线 E 于另一点 B,以 AB 为边作一个平行四边形,顶点 A、B、C、D 都在轨迹 E 上,判断平行四边形 ABCD 能否为菱形,并说明理由;
(3)当平行四边形 ABCD 的面积取到最大值时,判断它的形状,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
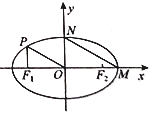
【题目】如图,椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,
, ![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
, ![]() 与
与![]() 轴垂直,且
轴垂直,且![]() .
.
(1)求椭圆的方程;
(2)过点![]() 且不垂直与坐标轴的直线与椭圆交于
且不垂直与坐标轴的直线与椭圆交于![]() ,
, ![]() 两点,已知点
两点,已知点![]() ,当
,当![]() 时,求满足
时,求满足![]() 的直线
的直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,已知但
,已知但![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 作斜率为的直线
作斜率为的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)当a>0时,解关于x的不等式f(x)<0;
(2)若当a>0时,f(x)<0在x![]() [1,2]上恒成立,求实数a的取值范围.
[1,2]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,an>0,(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,a3与a5的等比中项为2.
(1)求数列{an}的通项公式;
(2)设bn=log2an , 数列{bn}的前n项和为Sn , 当 ![]() 最大时,求n的值.
最大时,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com