
从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法有 种。
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
教育局组织直属学校的老师去新疆地区支教,现甲学校有2名男老师和3名女老师愿意去支教,乙学校有3名男老师和3名女老师愿意去支教,由于名额有限,教育局决定从甲学校选2人去支教,乙学校选1人去支教,若被选去支教的3名老师中必须有男老师,则乙学校被选去支教的老师是女老师的概率为
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
从红桃2、3、4、5和梅花2、3、4、5这8张扑克牌中取出4张排成一排,如果取出的4张扑克牌所标的数字之和等于14,则不同的排法共有 种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
关于二项式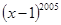 有下列命题:
有下列命题:
①该二项展开式中非常数项的系数和是1:
②该二项展开式中第六项为C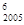
 ;
;
③该二项展开式中系数最大的项是第1002项:
④当x=2006时,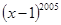 除以2006的余数是2005.
除以2006的余数是2005.
其中正确命题的序号是__________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com