
【题目】某辆汽车以![]() 千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求
千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求![]() )时,每小时的油耗(所需要的汽油量)为
)时,每小时的油耗(所需要的汽油量)为![]() 升,其中
升,其中![]() 为常数,且
为常数,且![]() .
.
(1)若汽车以![]() 千米/小时的速度行驶时,每小时的油耗为
千米/小时的速度行驶时,每小时的油耗为![]() 升,欲使每小时的油耗不超过
升,欲使每小时的油耗不超过![]() 升,求
升,求![]() 的取值范围;
的取值范围;
(2)求该汽车行驶![]() 千米的油耗的最小值.
千米的油耗的最小值.
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点为
的左右焦点为![]() 为它的中心,
为它的中心,![]() 为双曲线右支上的一点,
为双曲线右支上的一点,![]() 的内切圆圆心为
的内切圆圆心为![]() ,且圆
,且圆![]() 与
与![]() 轴相切于
轴相切于![]() 点,过
点,过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若双曲线的离心率为
,若双曲线的离心率为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 与
与![]() 关系不确定
关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在所有棱长都相等的三棱锥![]() 中,D,E,F分别是AB,BC,CA的中点,下列四个命题:
中,D,E,F分别是AB,BC,CA的中点,下列四个命题:
(1)![]() 平面PDF;(2)
平面PDF;(2)![]() 平面
平面![]() ;
;
(3)平面![]() 平面
平面![]() ;(4)平面
;(4)平面![]() 平面
平面![]() .
.
其中正确命题的序号为________.
A.(2)(3)B.(1)(3)C.(2)(4)D.(1)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为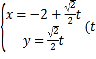 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
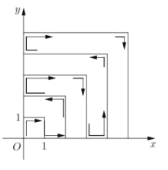
【题目】如图,一个粒子从原点出发,在第一象限和两坐标轴正半轴上运动,在第一秒时它从原点运动到点![]() ,接着它按图所示在
,接着它按图所示在![]() 轴、
轴、![]() 轴的垂直方向上来回运动,且每秒移动一个单位长度,那么,在2018秒时,这个粒子所处的位置在点______.
轴的垂直方向上来回运动,且每秒移动一个单位长度,那么,在2018秒时,这个粒子所处的位置在点______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,说法正确的个数是( )
(1)若p![]() q为真命题,则p,q均为真命题
q为真命题,则p,q均为真命题
(2)命题“x0∈R,![]() 0”的否定是“x∈R,2x
0”的否定是“x∈R,2x![]() 0”
0”
(3)“![]() ”是“x∈[1,2],x2﹣
”是“x∈[1,2],x2﹣![]() 恒成立”的充分条件
恒成立”的充分条件
(4)在△ABC中,“![]() ”是“sinA>sinB”的必要不充分条件
”是“sinA>sinB”的必要不充分条件
(5)命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com