
【题目】如图,在四棱锥![]() 中,底面为等腰梯形,且底面与侧面
中,底面为等腰梯形,且底面与侧面![]() 垂直,
垂直, ![]() ,
, ![]() 分别为线段
分别为线段![]() 的中点,
的中点, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据三角形中位线定理以及线面平行的判定定理可得![]() 与平面平面
与平面平面![]() 平行,从而可得平面
平行,从而可得平面![]() 平面
平面![]() ,进而根据面面平行的性质可得
,进而根据面面平行的性质可得![]() 平面
平面![]() ;(2)因为底面
;(2)因为底面![]() 与侧面
与侧面![]() 垂直,且
垂直,且![]() ,所以
,所以![]() 底面
底面![]() ,以
,以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() ,先求出
,先求出![]() 的方向向量,再根据向量垂直数量积为零列方程组求出平面
的方向向量,再根据向量垂直数量积为零列方程组求出平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果.
的一个法向量,根据空间向量夹角余弦公式,可得结果.
试题解析:(1)证明:因为![]() 分别为线段
分别为线段![]() 的中点,
的中点, ![]() ,所以
,所以![]() ,
, ![]() ,
,
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:因为底面![]() 与侧面
与侧面![]() 垂直,且
垂直,且![]() ,所以
,所以![]() 底面
底面![]() .
.
以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,
,

则![]() ,
, ![]() ,
, ![]() ,
, 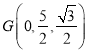 ,
,
所以![]() ,
, ![]() ,
, 
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() ,即
,即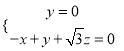 ,
,
故可取![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则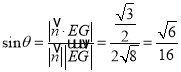 ,
,
故![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设△ABC中,角A,B,C所对的边分别为a,b,c,则“∠C>90°”的一个充分非必要条件是( )
A.sin2A+sin2B<sin2C
B.sinA= ![]() ,(A为锐角),cosB=
,(A为锐角),cosB= ![]()
C.c2>2(a+b﹣1)
D.sinA<cosB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据我国颁布的《环境空气质量指数(![]() )技术规定》 :空气质量指数划分为
)技术规定》 :空气质量指数划分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和大于300共六个等级,对应的空气质量指数的六个等级,指数越大,等级越高 ,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数不大于150时,可以进行户外活动;当空气质量指数为151及以上时,不适合进行旅游等户外活动,下表是某市2017年11月中旬的空气质量指数情况:
和大于300共六个等级,对应的空气质量指数的六个等级,指数越大,等级越高 ,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数不大于150时,可以进行户外活动;当空气质量指数为151及以上时,不适合进行旅游等户外活动,下表是某市2017年11月中旬的空气质量指数情况:
时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| 142 | 141 | 125 | 249 | 129 | 87 | 68 | 106 | 238 | 270 |
(1)该市某市民在上述10天中随机选取1天进行户外活动,求该市民选取的这一天恰好不适合进行户外活动的概率;
(2)一名外地游客计划在上述10天中到市连续旅游2天求这10天中适合他旅游的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}定义为a1>0,a11=a,an+1=an+ ![]() an2 , n∈N*
an2 , n∈N*
(1)若a1= ![]() (a>0),求
(a>0),求 ![]() +
+ ![]() +…+
+…+ ![]() 的值;
的值;
(2)当a>0时,定义数列{bn},b1=ak(k≥12),bn+1=﹣1+ ![]() ,是否存在正整数i,j(i≤j),使得bi+bj=a+
,是否存在正整数i,j(i≤j),使得bi+bj=a+ ![]() a2+
a2+ ![]() ﹣1.如果存在,求出一组(i,j),如果不存在,说明理由.
﹣1.如果存在,求出一组(i,j),如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点![]() ,一个焦点为
,一个焦点为![]() 的椭圆被直线
的椭圆被直线![]() 截得的弦的中点的横坐标为
截得的弦的中点的横坐标为![]() .
.
(1)求此椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() 两点,且以
两点,且以![]() 为对角线的菱形的一个顶点为
为对角线的菱形的一个顶点为![]() ,求
,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com