
【题目】已知圆![]() :
: ![]() 和抛物线
和抛物线![]() :
: ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)已知直线![]() 和圆
和圆![]() 相切,与抛物线
相切,与抛物线![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过抛物线![]() 上一点
上一点![]() 作两直线
作两直线![]() 和圆
和圆![]() 相切,且分别交抛物线
相切,且分别交抛物线![]() 于
于![]() 两点,若直线
两点,若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)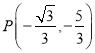 或
或![]() .
.
【解析】试题分析: 直线与圆相切只需圆心到直线的距离等于圆的半径,直线与曲线相交于![]() 两点,且满足
两点,且满足![]() ,只需数量积为0,要联立方程组设而不求,利用坐标关系及根与系数关系解题,这是解析几何常用解题方法,第二步利用直线
,只需数量积为0,要联立方程组设而不求,利用坐标关系及根与系数关系解题,这是解析几何常用解题方法,第二步利用直线![]() 的斜率找出坐标满足的要求,再利用两直线与圆相切,求出点的坐标.
的斜率找出坐标满足的要求,再利用两直线与圆相切,求出点的坐标.
试题解析:(1)解:设![]() ,
, ![]() ,
, ![]() ,由
,由![]() 和圆
和圆![]() 相切,得
相切,得![]() .
.
∴![]() .
.
由![]() 消去
消去![]() ,并整理得
,并整理得![]() ,
,
∴![]() ,
, ![]() .
.
由![]() ,得
,得![]() ,即
,即![]() .
.
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() 或
或![]() (舍).
(舍).
当![]() 时,
时, ![]() ,故直线
,故直线![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,
, ![]() ,则
,则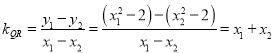 .
.
∴![]() .
.
设![]() ,由直线和圆相切,得
,由直线和圆相切,得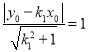 ,
,
即![]() .
.
设![]() ,同理可得:
,同理可得: ![]() .
.
故![]() 是方程
是方程![]() 的两根,故
的两根,故![]() .
.
由![]() 得
得![]() ,故
,故![]() .
.
同理![]() ,则
,则![]() ,即
,即![]() .
.
∴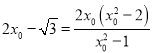 ,解
,解![]() 或
或![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
故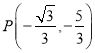 或
或![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图,OAB是一块半径为1,圆心角为 ![]() 的扇形空地.现决定在此空地上修建一个矩形的花坛CDEF,其中动点C在扇形的弧
的扇形空地.现决定在此空地上修建一个矩形的花坛CDEF,其中动点C在扇形的弧 ![]() 上,记∠COA=θ.
上,记∠COA=θ.
(Ⅰ)写出矩形CDEF的面积S与角θ之间的函数关系式;
(Ⅱ)当角θ取何值时,矩形CDEF的面积最大?并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P的坐标为(x﹣3,y﹣2).
(1)在一个盒子中,放有标号为1,2,3的三张卡片,现在从盒子中随机取出一张卡片,记下标号后把卡片放回盒中,再从盒子中随机取出一张卡片记下标号,记先后两次抽取卡片的标号分别为x、y,求点P在第二象限的概率;
(2)若利用计算机随机在区间[0,3]上先后取两个数分别记为x、y,求点P在第三象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为 ![]() 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
,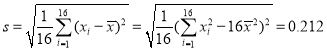 ,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ–3σ<Z<μ+3σ)=0.997 4,0.997 416≈0.959 2,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1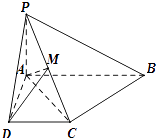
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB= ![]() ,EF=1,BC=
,EF=1,BC= ![]() ,且M是BD的中点..
,且M是BD的中点.. 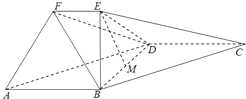
(1)求证:EM∥平面ADF;
(2)求直线DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com