
分析 bn的每4项求和的数列设为Cn,求bn前4t项之和就是求Cn前t项之和.由于bn是周期为4的似周期性等比数列,则$\frac{{B}_{n+4}}{{B}_{n}}$=3,所以$\frac{{C}_{n+1}}{{C}_{n}}$=3.由等比数列求和公式,即可得到所求和.
解答 解:把bn的每4项求和的数列设为Cn,
也就是说 C1=B1+B2+…+B4,Ct=B4t-3+B4t-2+…+B4t,
因此,求bn前4t项之和就是求Cn前t项之和.
由于bn是周期为4的似周期性等比数列,
则$\frac{{B}_{n+4}}{{B}_{n}}$=3,
所以$\frac{{C}_{n+1}}{{C}_{n}}$=3.
由等比数列求和公式,可得为c1+c2+c3+…+ct=$\frac{5(1-{3}^{t})}{1-3}$
=$\frac{5}{2}$(3t-1).
这就是数列bn前4t项之和,最后就是加上b4t+1,b4t+2这两项,
由于b4t+1=b1×3t=3t.b4t+2=b1×3t=3t.
因此,数列bn前4t+2项和就是$\frac{5}{2}$(3t-1)+3t+3t=$\frac{9}{2}•{3^t}-\frac{5}{2}$.
故答案为:$\frac{9}{2}•{3^t}-\frac{5}{2}$.
点评 本题主要考查数列与函数的综合、等比数列求和公式、新定义型问题的解决方法,考查运算求解能力、化归与转化思想,考查学生分析问题解决问题的能力和意识.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{2},+∞)$ | B. | $[-\frac{1}{2},2)$ | C. | $(-∞,-\frac{1}{2}]$ | D. | (-3,$-\frac{1}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
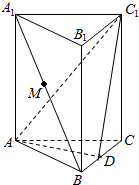 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,AA1=1,点D为BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,AA1=1,点D为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com