练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，已知抛物线，过抛物线上点B作切线交y轴于点

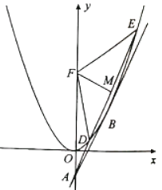
    （Ⅰ）求抛物线方程和切点的坐标；

    （Ⅱ）过点作抛物线的割线，在第一象限内的交点记为，，设为y轴上一点，满足，为中点，求的取值范围。

    【答案】（Ⅰ）抛物线方程为，切点（Ⅱ）

    【解析】

    (I)由直线与抛物线相切，则联立直线与抛物线方程，令即可求解；(II)联立直线与抛物线方程，因为两个交点，所以，即可得出的取值范围，利用弦长公式可得,由题意可知垂直平分，即可表示出，根据单调性即可求解范围.

    （Ⅰ）联立抛物线与直线的方程，

    得消去得，

    由，得，所以抛物线方程为，切点.

    （Ⅱ）设，，由题知，

    设，与抛物线联立，得，

    则，由及的条件可知，

    所以.

    易得，所以，

    所以.

    又因为，

    显然当时单调递增，所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆：，点，点是圆上任意一点，线段的垂直平分线交线段于点.

    （1）求点的轨迹方程.

    （2）设点，是的轨迹上异于顶点的任意两点，以为直径的圆过点.求证直线过定点，并求出该定点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数（，）.

    （1）当时，在上是单调递增函数，求的取值范围；

    （2）当时，讨论函数的单调区间；

    （3）对于任意给定的正实数，证明：存在实数，使得

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】影响消费水平的原因很多，其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法，在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平（单位：万元）.

    地区

    上海

    江苏

    浙江

    安徽

    福建

    职工平均工资

    9.8

    6.9

    6.4

    6.2

    5.6

    城镇居民消费水平

    6.6

    4.6

    4.4

    3.9

    3.8

    （1）利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平，求出线性回归方程，其中，；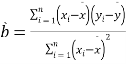

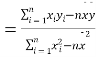    （2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万，则认为得到的线性回归方程是可靠的，试问所得的线性回归方程是否可靠？（的结果保留两位小数）

    （参考数据：，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为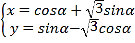（为参数），以坐标原点为极点，轴的正半轴为极轴，取相同长度单位建立极坐标系，直线的极坐标方程为.

    （Ⅰ）求曲线和直线的直角坐标方程；

    （Ⅱ）直线与轴交点为，经过点的直线与曲线交于，两点，证明：为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，半圆弧所在平面与平面垂直，且是上异于，的点，，，.

    （1）求证：平面；

    （2）若为的中点，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在三棱柱中，，，，分别为棱，的中点.

    （1）求证：平面；

    （2）若，，，求四棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC－A1B1C1中，AA1ABAC2，AB⊥AC，M是棱BC的中点点P在线段A1B上．

    （1）若P是线段A1B的中点，求直线MP与直线AC所成角的大小；

    （2）若是的中点，直线与平面所成角的正弦值为，求线段BP的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点在椭圆上，过点作轴于点

    （1）求线段的中点的轨迹的方程

    （2）设、两点在（1）中轨迹上，点，两直线与的斜率之积为，且（1）中轨迹上存在点满足，当面积最小时，求直线的方程．

    查看答案和解析>>

    同步练习册答案