
【题目】已知双曲线![]() -
-![]() =1(a>0,b>0)的离心率为2,焦点到渐近线的距离等于
=1(a>0,b>0)的离心率为2,焦点到渐近线的距离等于![]() ,过右焦点F2的直线l交双曲线于A,B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A,B两点,F1为左焦点.
(1)求双曲线的方程;
(2)若△F1AB的面积等于6![]() ,求直线l的方程.
,求直线l的方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.
(1)根据射击数据,计算红、蓝两个小组射击成绩的均值与方差,并说明红军还是蓝军的成绩相对比较稳定;
(2)若从蓝军6名士兵中随机抽取两人,求所抽取的两人的成绩之差不超过2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
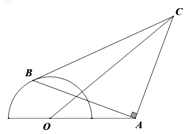
【题目】如图,半圆O的直径为2,A为直径延长线上一点,OA=2,B为半圆上任意一点,以线段AB为腰作等腰直角△ABC(C、O两点在直线AB的两侧),当∠AOB变化时,OC≤m恒成立,则m的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).

(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在 △ABC 中,设 a,b,c 分别是角 A,B,C 的对边,已知向量 ![]() = (a,sinC-sinB),
= (a,sinC-sinB),![]() = (b + c,sinA + sinB),且
= (b + c,sinA + sinB),且![]()
(1) 求角 C 的大小
(2) 若 c = 3, 求 △ABC 的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且a2=2,a4=![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]()
(3)试预测加工10个零件需要多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com