
科目:高中数学 来源:训练必修二数学人教A版 人教A版 题型:013
一个平面截空间四边形的四边得四个交点,如果该空间四边形仅有一条对角线与截面平行,那么此四个交点围成的四边形是
A.梯形
B.任意四边形
C.平行四边形
D.菱形
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)四边形MNPQ是平行四边形吗?
(2)若AC=BD,能截得菱形吗?如果能,那么如何截?
(3)在什么情况下,可以截得一个矩形?
(4)在什么条件下,能截得一个正方形?如果能,该怎样截?(注:只需给出满足条件的一种情形即可)
(5)若AC=BD=a,求证:四边形MNPQ的周长为定值.
查看答案和解析>>
科目:高中数学 来源:2014届山西省大同市高二第一次月考数学试卷(解析版) 题型:解答题
如图所示,四面体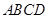 被一平面所截,截面
被一平面所截,截面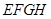 是一个平行四边形.求证:
是一个平行四边形.求证: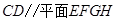 ;
;
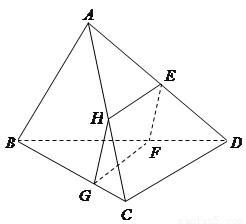
【答案】(理)证明: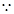 EH∥FG,EH
EH∥FG,EH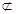 面
面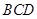 ,
,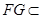 面
面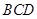
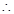 EH∥面
EH∥面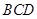 ,又
,又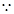 CD
CD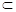 面
面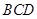 ,
,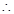 EH∥CD, 又EH
EH∥CD, 又EH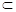 面EFGH,CD
面EFGH,CD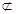 面EFGH
面EFGH
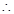 EH∥BD
EH∥BD
【解析】本试题主要是考查了空间四面体中线面位置关系的判定。
要证明线面平行可知通过线线平行,结合判定定理得到结论。
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高二上学期数学单元测试4 题型:解答题
|
 且
且
(Ⅰ)求k的值;
(Ⅱ)求
(文)某村计划建造一个室内面积为800m2的矩形蔬菜温室. 在温室内,种植蔬菜时需要沿左、右两侧与前侧内墙各保留1m宽的空地作为通道,后侧内墙不留空地(如图所示),问当温室的长是多少米时,能使蔬菜的种植面积最大?
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com