
【题目】已知向量![]() =(sinx,cosx),
=(sinx,cosx),![]() =(sin(x﹣
=(sin(x﹣![]() ),sinx),函数f(x)=2
),sinx),函数f(x)=2![]()
![]() ,g(x)=f(
,g(x)=f(![]() ).
).
(1)求f(x)在[![]() ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.
【答案】(1) ![]() .
.
(2) ![]() .
.
(3) g(x)2个零点.
【解析】
(1)根据向量的坐标运算,求出f(x)的表达式,再根据定义域求出最值及相应的自变量。
(2)根据三角函数表达式,求出三角函数的变化周期及函数值,代入求解。
(3)跟雷讨论在t取不同范围时,交点的个数问题。
(1)f(x)=2![]()
![]() =2sinxsin(x﹣
=2sinxsin(x﹣![]() )+2sinxcosx=
)+2sinxcosx=![]() sin2x+
sin2x+![]() sin2x
sin2x
=![]() sin2x﹣
sin2x﹣![]() cos2x+
cos2x+![]() =sin(2x﹣
=sin(2x﹣![]() )+
)+![]() ,
,
∵x∈[![]() ,π],∴
,π],∴![]() ≤2x﹣
≤2x﹣![]() ≤
≤![]() ,
,
∴﹣1≤sin(2x﹣![]() )≤
)≤![]() ,f(x)最小值为
,f(x)最小值为 ![]() ﹣1,f(x)最大值为
﹣1,f(x)最大值为 ![]() .
.
(2)由(1)得,f(x)=sin(2x﹣![]() )+
)+![]() .∴g(x)=f(
.∴g(x)=f(![]() )=sin(
)=sin(![]() x﹣
x﹣![]() )+
)+![]() .T=4,
.T=4,
∴g(1)+g(2)+g(3)+g(4)=g(5)+g(6)+g(7)+g(8)=…=g(2009)+g(2010)+g(2011)+g(2012).g(1)+g(2)+g(3)+g(4)=![]() ,g(1)+g(2)+g(3)+…+g(2014)=503×
,g(1)+g(2)+g(3)+…+g(2014)=503×![]() +g(1)+g(2)=1006
+g(1)+g(2)=1006![]() +
+![]() =
= ![]() .
.
(3)g(x)在[t,t+2]上零点的个数等价于y=sin(![]() x﹣
x﹣![]() )与y=﹣
)与y=﹣![]() 两图象交点个数.在同一直角坐标系内作出这两个数的图象.
两图象交点个数.在同一直角坐标系内作出这两个数的图象.
当4k<t<![]() +4k,k∈Z时,由图象可知,y=sin(
+4k,k∈Z时,由图象可知,y=sin(![]() x﹣
x﹣![]() )与y=﹣
)与y=﹣![]() 两图象无交点,g(x)无零点
两图象无交点,g(x)无零点
当![]() +4k≤t<2+4k或
+4k≤t<2+4k或![]() +4k<t≤4+4k时,y=sin(
+4k<t≤4+4k时,y=sin(![]() x﹣
x﹣![]() )与y=﹣
)与y=﹣![]() 两图象1个交点,g(x)1个零点
两图象1个交点,g(x)1个零点
当2+4k≤t≤![]() +4k时,y=sin(
+4k时,y=sin(![]() x﹣
x﹣![]() )与y=﹣
)与y=﹣![]() 两图象2个交点,g(x)2个零点.
两图象2个交点,g(x)2个零点.


科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),
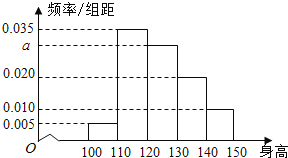
(1)由图中数据求a的值;
(2)若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为多少?
(3)估计这所小学的小学生身高的众数,中位数(保留两位小数)及平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是20个国家和地区的二氧化碳排放总量及人均二氧化碳排放量.
国家和地区 | 排放总量/千吨 | 人均排放量/吨 | 国家和地区 | 排放总量/千吨 | 人均排放量/吨 | |
A | 10330000 | 7.4 | K | 480000 | 2.0 | |
B | 5300000 | 16.6 | L | 480000 | 7.5 | |
C | 3740000 | 7.3 | M | 470000 | 3.9 | |
D | 2070000 | 1.7 | N | 410000 | 5.3 | |
E | 1800000 | 12.6 | O | 390000 | 16.9 | |
F | 1360000 | 10.7 | P | 390000 | 6.4 | |
G | 840000 | 10.2 | Q | 370000 | 5.7 | |
H | 630000 | 12.7 | R | 330000 | 6.2 | |
I | 550000 | 15.7 | S | 320000 | 6.2 | |
J | 510000 | 2.6 | T | 490000 | 16.6 |
(1)这20个国家和地区人均二氧化碳排放量的中位数是多少?
(2)针对这20个国家和地区,请你找出二氧化碳排放总量较少的前15%的国家和地区.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)写出直线l普通方程和曲线C的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”是我国数学史上的一个伟大成就,是二项式系数在三角形中的一种几何排列.如图所示,去除所有为1的项,依此构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前56项和为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x)=f(﹣4﹣x),f(0)=3,若![]() 是f(x)的两个零点,且
是f(x)的两个零点,且![]() .
.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若x>0,求g(x)=![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com