
���� ��1��������֪����$\overrightarrow{m}$•$\overrightarrow{n}$��Ȼ����������$\frac{1}{2}$������A��ֵ��
��2�������Ҷ���������֪��ʽ�ɵ�a2+c2-b2=ac���������Ҷ�������cosB����Ϸ�Χ����B��C�����ɵý⣮
��� �⣺��1����$\overrightarrow{m}$=��4��1����$\overrightarrow{n}$=��sin2$\frac{A}{2}$��cos2A����
$\overrightarrow{m}$•$\overrightarrow{n}$=4sin2$\frac{A}{2}$+cos2A��1�֣�
=2-2cosA+cos2A
=2cos2A-2cosA+1��3�֣�
����Ϊ$\overrightarrow{m}$•$\overrightarrow{n}$=$\frac{1}{2}$������$\frac{1}{2}$=2cos2A-2cosA+1��
���cosA=$\frac{1}{2}$��5�֣�
��0��A����
��A=$\frac{��}{3}$��6�֣�
��2����2bsinB=��2a-c��sinA+��2c-a��sinC��
�������Ҷ����ɵã�2b2=��2a-c��a+��2c-a��c�������ɵã�a2+c2-b2=ac��
�������Ҷ����ɵã�cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$����Ϸ�Χ��0��B���У����B=$\frac{��}{3}$��
���ã�C=A=B=$\frac{��}{3}$����ABCΪ�ȱ������Σ�
���� ������Ҫ������ƽ�����������������㣬���������Ҷ��������Ҷ������ۺ�Ӧ�ã������е��⣮


 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
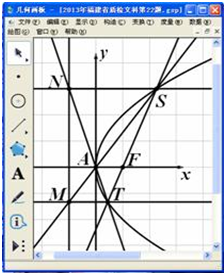 ijͬѧ�á����λ��塷�о������ߵ����ʣ������λ��塷����������ij������E��y2=2px���������������⻭һ����S��������S�����꣨xS��yS������ͼ��
ijͬѧ�á����λ��塷�о������ߵ����ʣ������λ��塷����������ij������E��y2=2px���������������⻭һ����S��������S�����꣨xS��yS������ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
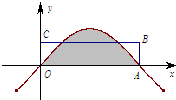 ��A�Ǻ���f��x��=sinx��ͼ����x���һ�����㣨��ͼ��ʾ������ͼ����Ӱ���ֵ�������ھ���OABC���������ô��AB�ij����ڣ�������
��A�Ǻ���f��x��=sinx��ͼ����x���һ�����㣨��ͼ��ʾ������ͼ����Ӱ���ֵ�������ھ���OABC���������ô��AB�ij����ڣ�������| A�� | $\frac{1}{��}$ | B�� | $\frac{2}{��}$ | C�� | $\frac{3}{��}$ | D�� | $\frac{4}{��}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1.5 | B�� | 3 | C�� | 0.5 | D�� | 3.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 3 | C�� | -$\frac{1}{3}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com