
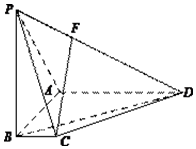
 如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.
如图,在四棱锥P-ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.分析 (Ⅰ)过点F作FH∥AD,交PA于H,连接BH,证明HF∥BC,CF∥BH,然后证明CF∥平面PAD.
(Ⅱ)说明BC⊥AB.PB⊥AB,PB⊥BC,以B为原点,BC,BA,BP所在直线为x,y,z轴建立空间直角坐标系,求出平面BPD的一个法向量,平面APD的一个法向量,通过向量的数量积求解二面角B-PD-A的大小.
解答 证明:(Ⅰ)过点F作FH∥AD,交PA于H,连接BH,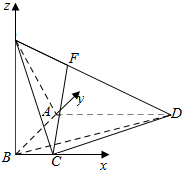
因为PF=$\frac{1}{3}$PD,所以HF=$\frac{1}{3}$AD=BC.….(1分)
又FH∥AD,AD∥BC,所以HF∥BC.….(2分)
所以BCFH为平行四边形,所以CF∥BH.….(3分)
又BH?平面PAB,CF?平面PAB,….(4分)(一个都没写的,则这(1分)不给)
所以CF∥平面PAB.….(5分)
解:(Ⅱ)因为梯形ABCD中,AD∥BC,AD⊥AB,所以BC⊥AB.
因为PB⊥平面ABCD,所以PB⊥AB,PB⊥BC,
如图,以B为原点,BC,BA,BP所在直线为x,y,z轴建立空间直角坐标系,….(6分)
所以C(1,0,0),D(3,3,0),A(0,3,0),P(0,0,3).
设平面BPD的一个法向量为$\overrightarrow{n}$=(x,y,z),平面APD的一个法向量为$\overrightarrow{m}$=(a,b,c),
因为$\overrightarrow{PD}$=(3,3,-3),$\overrightarrow{BP}$=(0,0,3)
所以$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PD}=3x+3y-3z=0}\\{\overrightarrow{n}•\overrightarrow{BP}=3z=0}\end{array}\right.$,….(7分)
取x=1得到$\overrightarrow{n}$=(1,-1,0),….(8分)
同理可得$\overrightarrow{m}$=(0,1,1),….(9分)
所以cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=-$\frac{1}{2}$,….(10分)
因为二面角B-PD-A为锐角,
所以二面角B-PD-A为$\frac{π}{3}$.….(12分)
点评 本题考查直线与平面平行的判定定理的应用,二面角的平面角的求法,向量的数量积的应用,考查空间想象能力以及计算能力.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
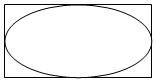 如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )
如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )| A. | 11 | B. | 9 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{5}{18}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com