
����Ŀ��2019��ȫ�������ᡱ�����л�������ʮ����ȫ���˴���λ�����й���������Э�̻����ʮ����ȫ��ίԱ��ڶ��λ��飬�ֱ���2019��3��5�պ�3��3���ڱ����ٿ�.Ϊ���˽���Щ�˸���ע�����ᡱ��ij���������ȡ��������15��75��֮���200�˽��е��飬����������Ƶ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ����������������[15��35)��[35��75]�ڵ��˷ֱ��Ϊ���������ˡ��͡��������ˡ�.��ͳ�ơ��������ˡ��͡��������ˡ�������֮��Ϊ19:21�����С��������ˡ�����40�˹�ע�����ᡱ�����������ˡ��й�ע�����ᡱ�Ͳ���ע�����ᡱ������֮����2:1.
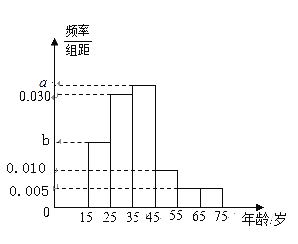
������ͼ��![]() ��ֵ��
��ֵ��
�����ֲ��÷ֲ������[25��35)��[45��55)�������ȡ8����������8������ѡ2�ˣ���2����������1���ǡ��������ˡ��ĸ����Ƕ���?
��������֪��������������2��2�������������ݴ�ͳ�ƽ���ж�:�ܷ���99.9%�İ�����Ϊ���������ˡ��ȡ��������ˡ����ӹ�ע�����ᡱ?
��ע | ����ע | �ϼ� | |
�������� | |||
�������� | |||
�ϼ� |
���𰸡�����![]() ����
����![]() ��������
��������
��������
������Ƶ�ʷֲ�ֱ��ͼ�з��̣���ý����������ö�ٷ��Լ��ŵ�����ʹ�ʽ�����������ȸ���������2��2���������ٸ��ݹ�ʽ�����������������ж�.
����������� ,���
,���![]()
�������������[25,35)�г�ȡ6�ˣ���Ϊ![]() ����[45,55)�г�ȡ2��, ��Ϊ
����[45,55)�г�ȡ2��, ��Ϊ![]() .
.
���8������ȡ2�˵�ȫ�������¼�(��28��)�о����£� ![]()
![]()
![]()
��2����������1���ǡ��������ˡ��ĸ�����![]() ����
����![]() .
.
����2��2���������£�
��ע | ����ע | �ϼ� | |
�������� | 40 | 55 | 95 |
�������� | 70 | 35 | 105 |
�ϼ� | 110 | 90 | 200 |
![]()
������99.9%�İ�����Ϊ�����������������������������ӹ�ע�����ᡱ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е�.
���е�.
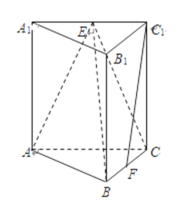
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����֤��![]() ƽ��
ƽ��![]() ��
��
��3��������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
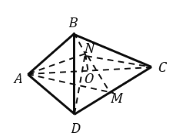
����Ŀ����֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() �ضԽ���
�ضԽ���![]() ����ʹƽ��
����ʹƽ��![]() ƽ��
ƽ��![]() ���õ���ͼ��ʾ������
���õ���ͼ��ʾ������![]() ����
����![]() Ϊ
Ϊ![]() �ߵ��е㣬
�ߵ��е㣬![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �ϵĶ��㣨�������˵㣩����
�ϵĶ��㣨�������˵㣩����![]() ����
����![]() ��������
��������![]() �����ȡ�����ֵʱ������
�����ȡ�����ֵʱ������![]() ��������İ뾶Ϊ_______.
��������İ뾶Ϊ_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=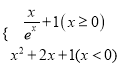 ��������y=f��f��x����a����1��������㣬��a��ȡֵ��Χ��_____��
��������y=f��f��x����a����1��������㣬��a��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ������
ʱ������![]() ��
��![]() �Ƿ������㣿������ڣ������㣻��������ڣ���˵�����ɣ�
�Ƿ������㣿������ڣ������㣻��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������3x+3y+8��2xy��x��0��y��0��������x��y����x+y��2��a��x+y��+16��0���������ʵ��a��ȡֵ��Χ�ǣ�������
A.��������8]B.[8��+����C.��������10]D.[10��+����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ϊ0�ĵȲ�����{an}����ǰn���ΪSn����S10��100��a1��a2��a5�ɵȱ����У�
��1����{an}��ͨ�ʽ��
��2��bn��anan+1+an+an+1+1��������![]() ��ǰn���Tn��
��ǰn���Tn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫���߹���(3����2)������Բ4x2��9y2��36����ͬ�Ľ��㣮
(1)��˫���ߵı����̣�
(2)����M��˫�����ϣ�F1��F2Ϊ���ҽ��㣬��|MF1|��|MF2|��6![]() �����б��MF1F2����״��
�����б��MF1F2����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��֪��Բ![]() ��
��![]() �dz����һ���˵㣬��
�dz����һ���˵㣬��![]() ����Բ������
����Բ������![]() ����
����![]() ��
��![]() .
.
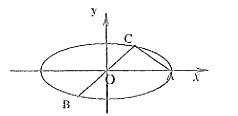
��������Բ�ķ��̣�
������![]() Ϊ��Բ������
Ϊ��Բ������![]() �Ҳ��غϵ����㣬��
�Ҳ��غϵ����㣬��![]() ��ƽ�������Ǵ�ֱ��
��ƽ�������Ǵ�ֱ��![]() �ᣬ�Ƿ����ʵ��
�ᣬ�Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() �����ֵ���������ڣ���˵������.
�����ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com