
分析 (1)案例一用简单随机抽样;案例二用分层抽样;案例三用系统抽样.
(2)按照分层、确定抽样比、确定各层样本数、按简单随机抽样方式在各层确定相应的样本、汇总构成一个容量为40的样本的过程求解即可.
(3)由已知条件利用系统抽样的方法步骤求解.
解答 解:(1)案例一中,因为总体单元数较少,用简单随机抽样;
案例二中,因为总体单位按职称特征分为四个层次,用分层抽样;
案例三中,因为总体单元数较多,用系统抽样.
(2)①分层,将总体分为高级职称、中级职称、初级职称及其余人员四层;
②确定抽样比例q=$\frac{40}{800}$=$\frac{1}{20}$;
③按上述比例确定各层样本数分别为8人、16人、10人、6人;
④按简单随机抽样方式在各层确定相应的样本;
⑤汇总构成一个容量为40的样本.
(3)K=3时,L+31K=18+31×3=111,故第三组样本编号为311.
K=8时,L+31K=18+31×8=266,故第8组样本编号为866.
点评 本题考查抽样方法的选择、分层抽样的步骤、系统抽样的方法,是基础题,解题时要认真审题,注意熟练掌握基本概念.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3,4} | B. | {2,3,5} | C. | {3,4,5} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
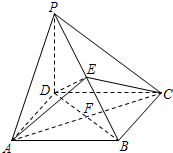 如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.求证:AC⊥DE.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.求证:AC⊥DE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)=0且f(x)为偶函数 | B. | f(-1)=0且f(x)为奇函数 | ||
| C. | f(x)为增函数且为奇函数 | D. | f(x)为增函数且为偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com