Question

20．已知曲线C_n的方程为：|x|ⁿ+|y|ⁿ=1（n∈N^*）．
（Ⅰ）分别求出n=1，n=2时，曲线C_n所围成的图形的面积；
（Ⅱ）若S_n（n∈N^*）表示曲线C_n所围成的图形的面积，求证：S_n（n∈N^*）关于n是递增的；
（Ⅲ） 若方程xⁿ+yⁿ=zⁿ（n＞2，n∈N），xyz≠0，没有正整数解，求证：曲线C_n（n＞2，n∈N^*）上任一点对应的坐标（x，y），x，y不能全是有理数．

Answer 1

分析 （Ⅰ）取n=1，n=2，得到C₁、C₂的方程，画出图象，结合图象求得面积；
（Ⅱ）要证 ${S_n}（n∈{N^*}）$是关于n递增的，只需证明：${S_n}＜{S_{n+1}}（n∈{N^*}）$．转化为证明曲线C_n在第一象限的部分与坐标轴所围成的面积递增．然后借助于函数单调性求证；
（Ⅲ） 由于xⁿ+yⁿ=zⁿ（n＞2，n∈N）可等价转化为${（\frac{x}{z}）^n}+{（\frac{y}{z}）^n}=1$，利用反证法证明曲线${（\frac{x}{z}）^n}+{（\frac{y}{z}）^n}=1$（n＞2，n∈N^*）上任一点对应的坐标（x，y），x，y不能全是有理数．

解答 （Ⅰ）解：当n=1，2时，曲线C₁、C₂的方程分别为|x|+|y|=1和x²+y²=1，
其图象分别如图：
由图可知${S}_{1}=\sqrt{2}×\sqrt{2}=2$，S₂=π；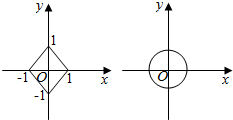
（Ⅱ）证明：要证 ${S_n}（n∈{N^*}）$是关于n递增的，只需证明：${S_n}＜{S_{n+1}}（n∈{N^*}）$．
由于曲线C_n具有对称性，只需证明曲线C_n在第一象限的部分与坐标轴所围成的面积递增．
现在考虑曲线C_n与C_n+1，
∵|x|ⁿ+|y|ⁿ=1（n∈N^*）…①，
∵|x|ⁿ⁺¹+|y|ⁿ⁺¹=1（n∈N^*）…②，
在①和②中令x=x₀，x₀∈（0，1），
当x₀∈（0，1），存在y₁，y₂∈（0，1）使得${x_0}^n+{y_1}^n=1$，${x_0}^{n+1}+{y_2}^{n+1}=1$成立，
此时必有y₂＞y₁．
∵当x₀∈（0，1）时${x_0}^n＞{x_0}^{n+1}$，
∴${y_2}^{n+1}＞{y_1}^n$．
两边同时开n次方有，${y_2}＞{y_2}^{\frac{n+1}{n}}＞{y_1}$．（指数函数单调性）
这就得到了y₂＞y₁，
从而${S_n}（n∈{N^*}）$是关于n递增的；
（Ⅲ）证明：由于xⁿ+yⁿ=zⁿ（n＞2，n∈N）可等价转化为${（\frac{x}{z}）^n}+{（\frac{y}{z}）^n}=1$，
反证：若曲线${C_n}（n＞2，n∈{N^*}）$上存在一点对应的坐标（x，y），x，y全是有理数，
不妨设$x=\frac{q}{p}，y=\frac{t}{s}$，p，q，s，t∈N^*，且p，q互质，s，t互质．
则由|x|ⁿ+|y|ⁿ=1可得，${|{\frac{q}{p}}|^n}+{|{\frac{t}{s}}|^n}=1$．
即|qs|ⁿ+|pt|ⁿ=|ps|ⁿ．
这时qs，pt，ps就是xⁿ+yⁿ=zⁿ（n＞2，n∈N^*）的一组解，
这与方程xⁿ+yⁿ=zⁿ（n＞2，n∈N^*），xyz≠0，没有正整数解矛盾，
∴曲线${C_n}（n＞2，n∈{N^*}）$上任一点对应的坐标（x，y），x，y不能全是有理数．

点评 本题考查曲线的方程和方程的曲线，考查逻辑思维能力和推理论证能力，考查数学转化思想方法，考查了反证法，是难题．