
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
|
|
| |||
| 0 |
|
|
|
|
| 0 | 3 | 0 | 0 |
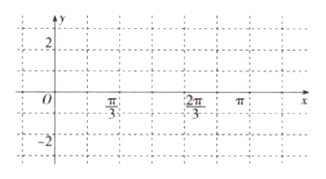
(1)请将上表数据补充完整,并写出函数![]() 的解析式(直接写出结果即可);
的解析式(直接写出结果即可);
(2)根据表格中的数据作出![]() 在一个周期内的图像;
在一个周期内的图像;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥S—ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,其中AB∥CD,∠ADC=90°,AD=AS=2,AB=1,CD=3,点E在棱CS上,且CE=λCS.
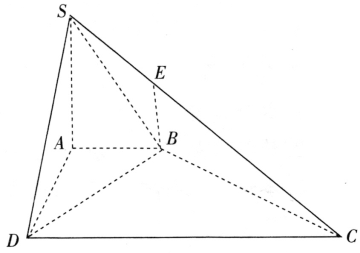
(1)若![]() ,证明:BE⊥CD;
,证明:BE⊥CD;
(2)若![]() ,求点E到平面SBD的距离.
,求点E到平面SBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线经过点
的抛物线经过点![]() 和
和![]() .
.
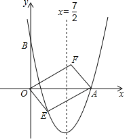
(1)求抛物线解析式及顶点坐标;
(2)设点![]() 是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,若点
,若点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() 是周长为
是周长为![]() 的正三角形.
的正三角形.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,抛物线在点
两点,抛物线在点![]() 处的切线与
处的切线与![]() 交于点
交于点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合计 | 20 | 60 | 80 |
(1)根据以上数据,能否有![]() 的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式与数据![]() 对应
对应![]() ,
,![]() 对应
对应![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com