[题目]定义在R上的偶函数f(x).对任意x1 . x2∈[0.+∞)(x1≠x2).有＜0.则( )A.fB.fC.fD.f 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】定义在R上的偶函数f（x），对任意x1 ， x2∈[0，+∞）（x1≠x2），有＜0，则（）
A.f（3）＜f（﹣2）＜f（1）
B.f（1）＜f（﹣2）＜f（3）
C.f（﹣2）＜f（1）＜f（3）
D.f（3）＜f（1）＜f（﹣2）

【答案】A
【解析】解：由题意，∵对任意x1 ， x2∈[0，+∞）（x1≠x2），有＜0，
∴函数在[0，+∞）上单调减
∴f（3）＜f（2）＜f（1）
∵函数是偶函数，∴f（﹣2）=f（2）
∴f（3）＜f（﹣2）＜f（1）
故选A．
【考点精析】掌握奇偶性与单调性的综合是解答本题的根本，需要知道奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知指数函数f（x）=ax（a＞0，a≠1）．
（1）若f（x）的图象过点（1，2），求其解析式；
（2）若，且不等式g（x2+x）＞g（3﹣x）成立，求实数x的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】莫数学建模兴趣小组测量某移动信号塔的高度（单位：），如图所示，垂直放置的标杆的高度，仰角， .

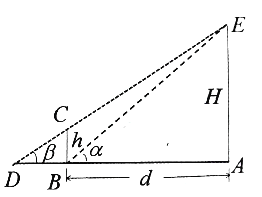
（Ⅰ）该小组已经测得一组的值，，，请推测的值；

（Ⅱ）该小组对测得的多组数据分析后，发现适当调节标杆到信号塔的距离（单位：），使得较大时，可以提高信号塔测量的精确度，若信号塔高度为，试问为多大时，最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某产品的三个质量指标分别为x，y，z，用综合指标S＝x＋y＋z评价该产品的等级．若S≤4, 则该产品为一等品．先从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如下：

产品编号	A1	A2	A3	A4	A5
质量指标 (x, y, z)	(1,1,2)	(2,1,1)	(2,2,2)	(1,1,1)	(1,2,1)
产品编号	A6	A7	A8	A9	A10
质量指标 (x, y, z)	(1,2,2)	(2,1,1)	(2,2,1)	(1,1,1)	(2,1,2)