
【题目】已知二次函数 f (x) = x 2 + x,若不等式 f (-x) + f (x)≤2 | x | 的解集为C. (1)求集合C (2)若方程 f (a x)-a x + 1 = 5(a > 0,a≠1)在 C上有解,求实数 a 的取值范围; (3)记 f (x) 在C 上的值域为 A,若 g(x) = x 3-3tx + ![]() ,x∈[0,1] 的值域为B,且 A B,求实数 t 的取值范围.
,x∈[0,1] 的值域为B,且 A B,求实数 t 的取值范围.
【答案】(1)[-1,1](2)0 < a≤![]() 或 a≥5(3)
或 a≥5(3)![]()
【解析】试题分析:(1)根据绝对值定义将不等式化为两个不等式组,分别求解,最后求并集(2)将方程转化为关于![]() 二次方程,根据底与1的大小分类讨论方程有解的条件,结合零点存在定理实数 a 的取值范围;(3)先利用导数研究函数g(x)单调性,确定其值域,再根据A B,利用数轴列条件,求实数 t 的取值范围.
二次方程,根据底与1的大小分类讨论方程有解的条件,结合零点存在定理实数 a 的取值范围;(3)先利用导数研究函数g(x)单调性,确定其值域,再根据A B,利用数轴列条件,求实数 t 的取值范围.
试题解析:解:(1) f (x) + f (-x) = 2x 2
当 x≥0时,2x 2≤2x 0≤x≤1
当 x < 0时, 2x 2≤-2x -1≤x < 0
∴集合 C = [-1,1]
(2) f (a x)-a x + 1-5 = 0 (a x) 2-(a-1)a x-5 = 0,令 a x = u
则方程为 h(u) = u 2-(a-1)u-5 = 0 h(0) = -5
当 a > 1时,u∈[![]() ,a],h(u) = 0 在 [
,a],h(u) = 0 在 [![]() ,a] 上有解,
,a] 上有解,
则 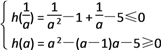 a≥5
a≥5
当 0 < a < 1时,u∈[a,![]() ],h(u) = 0 在 [a,
],h(u) = 0 在 [a,![]() ]上有解,
]上有解,
则 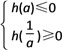 0 < a≤
0 < a≤![]()
∴当 0 < a≤![]() 或 a≥5时,方程在C上有解,且有唯一解。
或 a≥5时,方程在C上有解,且有唯一解。
(3) A = [-![]() ,2]
,2]
∵![]() ,∴
,∴ ![]() .
.
①当 t≤0时,函数 g(x) = x 3-3tx +![]() 在 x∈[0,1]单调递增,
在 x∈[0,1]单调递增,
∴函数 g(x)的值域 B =[![]() ,
,![]() ],
],
∵ A B ,∴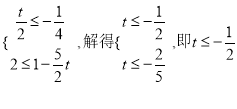 ,
,
②当t≥1时,令![]() ,得函数 g(x)的单调递减区间为:
,得函数 g(x)的单调递减区间为: ![]() ,
,
∵![]()
∴函数 g(x)在区间 [0,1]单调递减, B = [![]() ]
]
∴
![]()
③当 0 < t < 1 时,同理可得:
函数 g(x)的单调递减区间为: ![]() ;g(x)的单调递增区间为:[
;g(x)的单调递增区间为:[![]() ,1].
,1].
g(x)在 x =![]() 达到最小值。
达到最小值。
要使 A B,则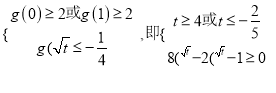
∵0 < t < 1,所以使得 A B的 t无解。
综上所述:t的取值范围是: ![]()


科目:高中数学 来源: 题型:
【题目】某辆汽车以x km/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为![]() ,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.
,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.
(1)求k的值;
(2)求该汽车每小时油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用an的信息如图. 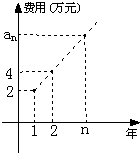
(1)求an;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥D﹣ABC中,AB=BC=1,AD=2,BD= ![]() ,AC=
,AC= ![]() ,BC⊥AD,则三棱锥的外接球的表面积为( )
,BC⊥AD,则三棱锥的外接球的表面积为( )
A.![]() π
π
B.6π
C.5π
D.8π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
: ![]() 和圆
和圆![]() :
: ![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设![]() 为平面直角坐标系上的点,满足:存在过点
为平面直角坐标系上的点,满足:存在过点![]() 的无穷多对相互垂直的直线
的无穷多对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和
和![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是空间两条直线,
是空间两条直线, ![]() 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )
A. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,我们把使
,我们把使![]() 的实数
的实数![]() 叫做函数
叫做函数![]() 的零点,且有如下零
的零点,且有如下零
点存在定理:如果函数![]() 在区间
在区间![]() 上的图像是连续不断的一条曲线,并且有
上的图像是连续不断的一条曲线,并且有![]() ,那么,函数
,那么,函数![]() 在区间
在区间![]() 内有零点.给出下列命题:
内有零点.给出下列命题:
①若函数![]() 在
在![]() 上是单调函数,则
上是单调函数,则![]() 在
在![]() 上有且仅有一个零点;
上有且仅有一个零点;
②函数![]() 有
有![]() 个零点;
个零点;
③函数![]() 和
和![]() 的图像的交点有且只有一个;
的图像的交点有且只有一个;
④设函数![]() 对
对![]() 都满足
都满足![]() ,且函数
,且函数![]() 恰有
恰有![]() 个不同的零点,则这6个零点的和为18;
个不同的零点,则这6个零点的和为18;
其中所有正确命题的序号为________.(把所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题: 1)y=|cos(2x+ ![]() )|最小正周期为π;
)|最小正周期为π;
2)函数y=tan ![]() 的图象的对称中心是(kπ,0),k∈Z;
的图象的对称中心是(kπ,0),k∈Z;
3)f(x)=tanx﹣sinx在(﹣ ![]() ,
, ![]() )上有3个零点;
)上有3个零点;
4)若 ![]() ∥
∥ ![]() ,
, ![]() ,则
,则 ![]()
其中错误的是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com