
下列叙述正确的序号是 。
(1)对于定义在R上的函数 ,若
,若 ,则函数
,则函数 不是奇函数;
不是奇函数;
(2) 定义在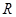 上的函数
上的函数 ,在区间
,在区间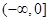 上是单调增函数,在区间
上是单调增函数,在区间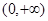 上也是单调增函数,则函数
上也是单调增函数,则函数 在
在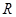 上是单调增函数;
上是单调增函数;
(3) 已知函数的解析式为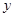 =
=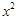 ,它的值域为
,它的值域为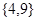 ,那么这样的函数有9个;
,那么这样的函数有9个;
(4)对于任意的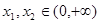 ,若函数
,若函数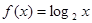 ,则
,则
(3),(4)
解析试题分析:(1)函数y=0(x∈R)既是奇函数又是偶函数,但f(3)=f(-3),故不对;(2)由增函数的定义中“任意性”知,两个单调区间不能并在一起,故不对;(3)∵函数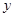 =
=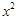 的值域为
的值域为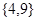 ,∴x的取值集合为{-2,2,3,-3}、{-2,2,3}、{-2,2,-3}、{2,3,-3}、{-2,3,-3}、{2,3 }、{2, -3}、{-2,3 }、{-2,-3}共计9个,所以符合题意的函数有9个,故正确;(4)∵
,∴x的取值集合为{-2,2,3,-3}、{-2,2,3}、{-2,2,-3}、{2,3,-3}、{-2,3,-3}、{2,3 }、{2, -3}、{-2,3 }、{-2,-3}共计9个,所以符合题意的函数有9个,故正确;(4)∵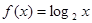 在
在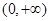 上单调递增且为上凸函数,∴
上单调递增且为上凸函数,∴ ,故正确。
,故正确。
考点:本题考查了函数的单调性
点评:奇(偶)函数和增函数的定义的应用试题,主要考查对定义中关键词“任意性”的理解


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的________条件.(填充分必要条件,充分不必要条件,必要不充分条件,既不充分又不必要条件之一)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列四个命题:
①若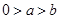 ,则
,则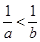 ;
;
②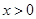 ,
,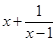 的最小值为
的最小值为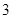 ;
;
③椭圆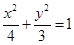 比椭圆
比椭圆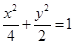 更接近于圆;
更接近于圆;
④设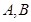 为平面内两个定点,若有
为平面内两个定点,若有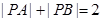 ,则动点
,则动点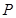 的轨迹是椭圆;
的轨迹是椭圆;
其中真命题的序号为________________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列四个命题:
(1)方程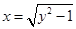 表示双曲线的一部分;
表示双曲线的一部分;
(2)动点到两个定点的距离之和为定长,则动点的轨迹为椭圆;
(3)动点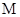 与点
与点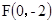 的距离比它到直线
的距离比它到直线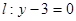 的距离小1的轨迹方程是
的距离小1的轨迹方程是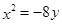 ;
;
(4)若双曲线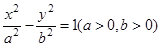 的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点
的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点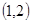 在“上”区域内,则双曲线的离心率
在“上”区域内,则双曲线的离心率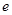 的取值范围是
的取值范围是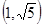 .其中所有正确命题的序号是 .
.其中所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列命题:
①存在实数 ,使得
,使得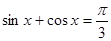 ;
;
②函数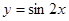 的图象向右平移
的图象向右平移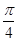 个单位,得到
个单位,得到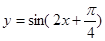 的图象;
的图象;
③函数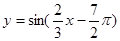 是偶函数;
是偶函数;
④已知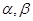 是锐角三角形ABC的两个内角,则
是锐角三角形ABC的两个内角,则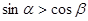 。
。
其中正确的命题的个数为
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列命题:
①函数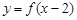 与函数
与函数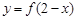 的图象关于
的图象关于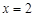 对称
对称
②函数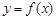 导函数为
导函数为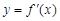 ,若
,若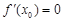 ,则
,则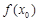 必为函数
必为函数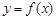 的极值.
的极值.
③函数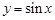 在一象限单调递增
在一象限单调递增
④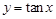 在其定义域内为单调增函数.
在其定义域内为单调增函数.
其中正确的命题序号为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com