
 .
. )时,f'(x)>0.
)时,f'(x)>0. )时,f'(x)g'(x)<0.故由题设得a≥-
)时,f'(x)g'(x)<0.故由题设得a≥- 且b≥-
且b≥- ,
, ≤a<0,于是-
≤a<0,于是- <b<0,因此|a-b|≤
<b<0,因此|a-b|≤ ,且当a=-
,且当a=- ,b=0时等号成立,
,b=0时等号成立, ,b=0时,f'(x)g'(x)=6x(x2-
,b=0时,f'(x)g'(x)=6x(x2- ),从而当x∈(-
),从而当x∈(- ,0)时f'(x)g'(x)>0.
,0)时f'(x)g'(x)>0. ,0)上单调性一致,因此|a-b|的最大值为
,0)上单调性一致,因此|a-b|的最大值为 .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| e1 |
| e2 |
| 1 | ||||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省石家庄市高三下学期第二次质量检测文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函數f(x)=ln+mx2(m∈R)
(I)求函数f(x)的单调区间;
(II)若A,B是函数f(x)图象上不同的两点,且直线AB的斜率恒大于1,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a-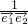 是偶函数.
是偶函数.查看答案和解析>>
科目:高中数学 来源:2011年上海市黄浦区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
 =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a- 是偶函数.
是偶函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com