
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,求实教a,b的值.
,求实教a,b的值.
(2)若![]() ,且
,且![]() 对一切正实数x值成立,求实数b的取值范围.
对一切正实数x值成立,求实数b的取值范围.
(3)若![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)利用导数的几何意义即可;
(2)分离参数,构造函数,利用导数求出函数的最值即可;
(3)对a分![]() ,
,![]() ,
,![]() ,
,![]() 四种情况讨论即可.
四种情况讨论即可.
(1)![]() ,由题意
,由题意![]() ,即
,即![]() ,解得
,解得![]() ;
;
(2)当![]() 时,
时,![]() ,
,![]() 对一切正实数x值成立,即
对一切正实数x值成立,即
![]() 对一切正实数x值成立,
对一切正实数x值成立,
设![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,
,
由![]() 得
得![]() ,故
,故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
所以![]() ,所以
,所以![]() ;
;
(3)当![]() 时,
时,![]() ,
,![]() ,
,
令![]()
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,![]() ,所以
,所以![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
若![]() ,由
,由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ;
;
综上,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ;
;


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:千人) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根据表中的数据判断从2014年到2019年哪个跨年度的人口增长数量最大?并描述该地人口数量的变化趋势;
(2)研究人员用函数![]() 拟合该地的人口数量,其中
拟合该地的人口数量,其中![]() 的单位是年,2014年年初对应时刻
的单位是年,2014年年初对应时刻![]() ,
,![]() 的单位是千人,经计算可得
的单位是千人,经计算可得![]() ,请解释
,请解释![]() 的实际意义.
的实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,△ABC是边长为6的等边三角形,D,E分别为AA1,BC的中点.
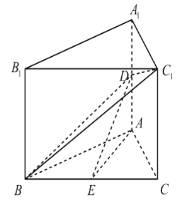
(1)证明:AE//平面BDC1;
(2)若异面直线BC1与AC所成角的余弦值为![]() .求DE与平面BDC1所成角的正弦值.
.求DE与平面BDC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)直线![]() 在矩阵
在矩阵![]() 所对应的变换
所对应的变换![]() 下得到直线
下得到直线![]() ,求
,求![]() 的方程.
的方程.
(2)已知点![]() 是曲线
是曲线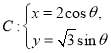 (
(![]() 为参数,
为参数,![]() )上一点,
)上一点,![]() 为坐标原点直线
为坐标原点直线![]() 的倾斜角为
的倾斜角为![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值.经数据处理后得到该样本的频率分布直方图,其中质量指标值不大于1.50的茎叶图如图所示,以这100件产品的质量指标值在各区间内的频率代替相应区间的概率.
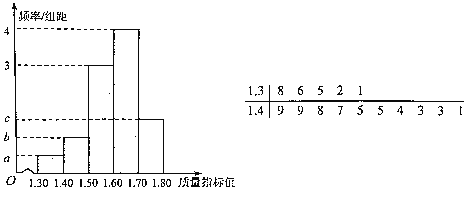
(1)求图中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计这种产品质量指标值的平均数及方差(说明:①同一组中的数据用该组区间的中点值作代表;②方差的计算只需列式正确);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于1.50的产品至少要占全部产品的![]() ”的规定?
”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
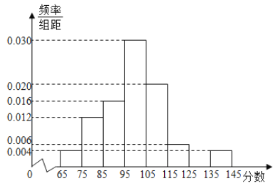
(1)求第七组的频率;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线斜率为0.函数
处的切线斜率为0.函数![]()
(1)试用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)求![]() 的单调区间;
的单调区间;
(3)令![]() ,设函数
,设函数![]() 在
在![]()
![]() 处取得极值,记点
处取得极值,记点![]() ,
,![]() ,证明:线段
,证明:线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() ,
,![]() 的公共点.
的公共点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com