
【题目】某工厂的一台某型号机器有2种工作状态:正常状态和故障状态.若机器处于故障状态,则停机检修.为了检查机器工作状态是否正常,工厂随机统计了该机器以往正常工作状态下生产的1000个产品的质量指标值,得出如图1所示频率分布直方图.由统计结果可以认为,这种产品的质量指标值服从正态分布![]() ,其中
,其中![]() 近似为这1000个产品的质量指标值的平均数
近似为这1000个产品的质量指标值的平均数![]() ,
,![]() 近似为这1000个产品的质量指标值的方差
近似为这1000个产品的质量指标值的方差![]() (同一组中的数据用该组区间中点值为代表).若产品的质量指标值全部在
(同一组中的数据用该组区间中点值为代表).若产品的质量指标值全部在![]() 之内,就认为机器处于正常状态,否则,认为机器处于故障状态.
之内,就认为机器处于正常状态,否则,认为机器处于故障状态.
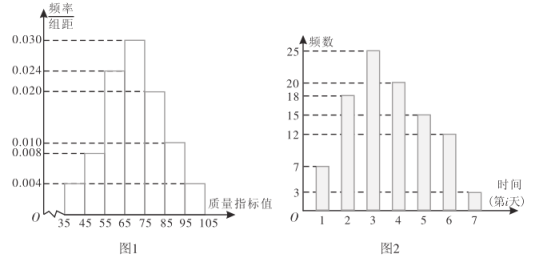
(1)下面是检验员在一天内从该机器生产的产品中随机抽取10件测得的质量指标值:
29 45 55 63 67 73 78 87 93 113
请判断该机器是否出现故障?
(2)若机器出现故障,有2种检修方案可供选择:
方案一:加急检修,检修公司会在当天排除故障,费用为700元;
方案二:常规检修,检修公司会在七天内的任意一天来排除故障,费用为200元.
现需决策在机器出现故障时,该工厂选择何种方案进行检修,为此搜集检修公司对该型号机器近100单常规检修在第i(![]() ,2,…,7)天检修的单数,得到如图2所示柱状图,将第i天常规检修单数的频率代替概率.已知该机器正常工作一天可收益200元,故障机器检修当天不工作,若机器出现故障,该选择哪种检修方案?
,2,…,7)天检修的单数,得到如图2所示柱状图,将第i天常规检修单数的频率代替概率.已知该机器正常工作一天可收益200元,故障机器检修当天不工作,若机器出现故障,该选择哪种检修方案?
附:![]() ,
,![]() ,
,![]() .
.
【答案】(1)可判断该机器处于故障状态;(2)选择加急检修更为适合
【解析】
(1)由图1可估计1000个产品的质量指标值的平均数![]() 和方差
和方差![]() ,所以
,所以![]() ,
,![]() ,从而得到产品的质量指标值允许落在的范围为(28.87,111.13),由于抽取产品质量指标值出现了113,不在(28.87,111.13)之内,故机器处于故障状态;
,从而得到产品的质量指标值允许落在的范围为(28.87,111.13),由于抽取产品质量指标值出现了113,不在(28.87,111.13)之内,故机器处于故障状态;
(2)方案一:工厂需要支付检修费和损失收益之和为700+200=900元;方案二:设损失收益为![]() 元,求出
元,求出![]() 的可能值,然后由图2可得出每个
的可能值,然后由图2可得出每个![]() 的取值所对应的概率,求出数学期望,可得工厂需要支付检修费和损失收益之和,与900对比,即可得出结论.
的取值所对应的概率,求出数学期望,可得工厂需要支付检修费和损失收益之和,与900对比,即可得出结论.
(1)由图1可估计1000个产品质量指标值的平均数![]() 和方差
和方差![]() 分别为
分别为
![]() ,
,![]()
![]() ,
,
依题意知,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以产品质量指标值允许落在的范围为![]() ,
,
又抽取产品质量指标值出现了113,不在![]() 之内,
之内,
故可判断该机器处于故障状态;
(2)方案一:若安排加急检修,工厂需要支付检修费和损失收益之和为![]() 元;
元;
方案二:若安排常规检修,工厂需要要支付检修费为200元,
设损失收益为X元,则X的可能取值为200,400,600,800,1000,1200,1400,
X的分布列为:
X | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 |
P | 0.07 | 0.18 | 0.25 | 0.20 | 0.15 | 0.12 | 0.03 |
![]()
![]() 元;
元;
故需要支付检修费和损失收益之和为![]() 元,
元,
因为![]() ,所以当机器出现故障,选择加急检修更为适合.
,所以当机器出现故障,选择加急检修更为适合.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,
,![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求数列![]() ,
,![]() 的通项公式.
的通项公式.
(2)设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() .
.
(3)设![]() ,求数列
,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() 的反函数.定义:若对给定的实数
的反函数.定义:若对给定的实数![]() ,函数
,函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 和性质”;若函数
和性质”;若函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足“
满足“![]() 积性质”.
积性质”.
(1) 判断函数![]() 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2) 求所有满足“2和性质”的一次函数;
(3) 设函数![]() 对任何
对任何![]() ,满足“
,满足“![]() 积性质”.求
积性质”.求![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是从2020年2月14日至2020年4月19日共66天的新冠肺炎中国/海外新增确诊趋势图,根据该图,下列结论中错误的是( )
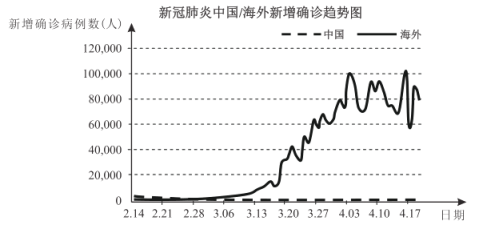
A.从2020年2月14日起中国已经基本控制住国内的新冠肺炎疫情
B.从2020年3月13日至2020年4月3日海外新冠肺炎疫情快速恶化
C.这66天海外每天新增新冠肺炎确诊病例数的中位数在区间![]() 内
内
D.海外新增新冠肺炎确诊病例数最多的一天突破10万例
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为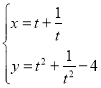 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,(
,(![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求线段
两点,求线段![]() 的长度
的长度![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.

(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率.
(2)求取出的4个球中恰有1个红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com