
【题目】已知函数f(x)=ax﹣x2﹣lnx存在极值,若这些极值的和大于5+ln2,则实数a的取值范围为( )
A.(﹣∞,4)
B.(4,+∞)
C.(﹣∞,2)
D.(2,+∞)
【答案】B
【解析】解:f(x)=ax﹣x2﹣lnx,x∈(0,+∞), 则f′(x)=a﹣2x﹣ ![]() =﹣
=﹣ ![]() ,
,
∵函数f(x)存在极值,∴f′(x)=0在(0,+∞)上有根,
即2x2﹣ax+1=0在(0,+∞)上有根,∴△=a2﹣8≥0,
显然当△=0时,F(x)无极值,不合题意;
∴方程必有两个不等正根,记方程2x2﹣ax+1=0的两根为x1 , x2 , x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
f(x1),f(x2)是函数F(x)的两个极值,
由题意得,f(x1)+f(x2)=a(x1+x2)﹣(x12+x22)﹣(lnx1+lnx2)
= ![]() ﹣
﹣ ![]() +1﹣ln
+1﹣ln ![]() >5﹣ln
>5﹣ln ![]() ,
,
化简解得,a2>16,满足△>0,
又x1+x2= ![]() >0,即a>0,
>0,即a>0,
∴∴a的取值范围是(4,+∞),
故选:B.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,过对角线
中,过对角线![]() 的一个平面交
的一个平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
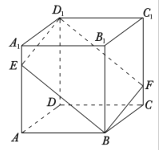
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能是正方形;
有可能是正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④四边形![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
以上结论正确的为_______________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣1|,a∈R.
(Ⅰ)若不等式f(x)≥2﹣|x﹣1|恒成立,求实数a的取值范围;
(Ⅱ)当a=1时,直线y=m与函数f(x)的图象围成三角形,求m的最大值及此时围成的三角形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() :
: ![]() ,右顶点为
,右顶点为 ![]() ,离心率为
,离心率为 ![]() ,直线
,直线 ![]() :
: ![]() 与椭圆
与椭圆 ![]() 相交于不同的两点
相交于不同的两点 ![]() ,
, ![]() ,过
,过 ![]() 的中点
的中点 ![]() 作垂直于
作垂直于 ![]() 的直线
的直线 ![]() ,设
,设 ![]() 与椭圆
与椭圆 ![]() 相交于不同的两点
相交于不同的两点 ![]() ,
, ![]() ,且
,且 ![]() 的中点为
的中点为 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设原点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是东西方向的公路北侧的边缘线,某公司准备在
是东西方向的公路北侧的边缘线,某公司准备在![]() 上的一点
上的一点![]() 的正北方向的
的正北方向的![]() 处建一仓库,并在公路同侧建造一个正方形无顶中转站
处建一仓库,并在公路同侧建造一个正方形无顶中转站![]() (其中边
(其中边![]() 在
在![]() 上),现从仓库
上),现从仓库![]() 向
向![]() 和中转站分别修两条道路
和中转站分别修两条道路![]() ,
,![]() ,已知
,已知![]() ,且
,且![]() ,设
,设![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果中转站四周围墙(即正方形周长)造价为![]() 万元
万元![]() ,两条道路造价为
,两条道路造价为![]() 万元
万元![]() ,问:
,问:![]() 取何值时,该公司建中转围墙和两条道路总造价
取何值时,该公司建中转围墙和两条道路总造价![]() 最低?
最低?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com