
| A. | (0,$\frac{1}{3}$] | B. | [$\frac{1}{3}$,1) | C. | (0,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,1) |
分析 根据f(x)在R上单调,可知a<1,那么-4a<0,且满足(ax-2a)max≤(-4ax+a)min可得a的取值范围.
解答 解:函数f(x)$\left\{\begin{array}{l}{{a}^{x}-2a,x>0}\\{-4ax+a,x≤0}\end{array}\right.$,其中a>0,且a≠1,
f(x)在R上单调,观察选项,可知:y=ax-2a是减函数,则a<1.
∴y=-4ax+a也是减函数,则-4a<0,即a>0.
且满足(ax-2a)max≤(-4ax+a)min,可得:1-2a≤a,
解得:$a≥\frac{1}{3}$.
综上可得:a的取值范围是[$\frac{1}{3}$,1).
故选B.
点评 本题考查了分段函数的单调性的运用.属于基础题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
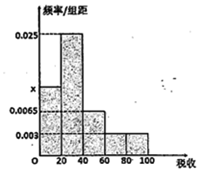 我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $1-\frac{{\sqrt{3}}}{2}$ | D. | $1-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
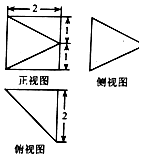
| A. | $\frac{8}{3}$ | B. | 4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | λ先变小再变大 | |
| B. | 仅当M为线段EF的中点时,λ取得最大值 | |
| C. | λ先变大再变小 | |
| D. | λ是一个定值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com