
【题目】如图,在四棱锥 ![]() 中,底面
中,底面 ![]() 为矩形,
为矩形, ![]() 是
是 ![]() 的中点,
的中点, ![]() 是
是 ![]() 的中点,
的中点, ![]() 是
是 ![]() 中点.
中点.
(1)证明: ![]() 平面
平面 ![]() ;
;
(2)若平面 ![]() 底面
底面 ![]() ,
, ![]() ,试在
,试在 ![]() 上找一点
上找一点 ![]() ,使
,使 ![]() 平面
平面 ![]() ,并证明此结论.
,并证明此结论.
【答案】
(1)证明:连接 ![]() ,交
,交 ![]() 于点
于点 ![]() ,连接
,连接 ![]() .
.
∵四边形 ![]() 为矩形,
为矩形,
∴ ![]() 为
为 ![]() 的中点.
的中点.
又 ![]() 为
为 ![]() 的中点,∴
的中点,∴ ![]() .
.
又 ![]() 是
是 ![]() 的中点,
的中点, ![]() 是
是 ![]() 中点,∴
中点,∴ ![]() ,∴
,∴ ![]() .
.
∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
∴ ![]() 平面
平面 ![]()
(2)解: ![]() 的中点
的中点 ![]() 即为所求的点.
即为所求的点.
证明如下:
连接 ![]() ,
,
∵ ![]() 为
为 ![]() 的中点,∴
的中点,∴ ![]() ,
, ![]() .
.
又 ![]() 为
为 ![]() 的中点,且四边形
的中点,且四边形 ![]() 为矩形,
为矩形,
∴ ![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() .
.
∴四边形 ![]() 为平行四边形,∴
为平行四边形,∴ ![]() .
.
∵平面 ![]() 底面
底面 ![]() ,平面
,平面 ![]() 底面
底面 ![]() ,
, ![]() 底面
底面 ![]() ,
, ![]() ,
,
∴ ![]() 平面
平面 ![]() ,
,
又 ![]() 平面
平面 ![]() ,∴
,∴ ![]() .∴
.∴ ![]() .
.
又∵ ![]() ,
, ![]() 是
是 ![]() 的中点,∴
的中点,∴ ![]() ,∴
,∴ ![]() .
.
又 ![]() 平面
平面 ![]() ,
, ![]() ,∴
,∴ ![]() 平面
平面 ![]() .
.
PC 的中点 G 即为所求的点.
【解析】(1)证明线面平行的要点是在平面中找到一条与所证直线平行的直线;
(2)探索直线上一点使线面垂直,可先找到一点,再利用判定定理进行证明.


科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,向量
项和,向量![]() ,
,![]() ,
,
![]() .
.
(1)若![]() ,求数列
,求数列![]() 通项公式;
通项公式;
(2)若![]() ,
,![]() .
.
①证明:数列![]() 为等差数列;
为等差数列;
②设数列![]() 满足
满足![]() ,问是否存在正整数
,问是否存在正整数![]() ,
,![]() ,且
,且![]() ,
,![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,若存在,求出
成等比数列,若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字![]() ,
,![]() ,
,![]() ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|(x﹣2)(x+3)<0},B={x|y= ![]() },则A∩(RB)=( )
},则A∩(RB)=( )
A.[﹣3,﹣1]
B.(﹣3,﹣1]
C.(﹣3,﹣1)
D.[﹣1,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积问题,意思是两个等高的几何体,如在同高处的截面积恒相等,则体积相等,设A,B为两个等高的几何体,p:A,B的体积相等,q:A,B在同高处的截面积不恒相等,根据祖暅原理可知,q是-p的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)当a>0时,解关于x的不等式f(x)<0;
(2)若当a>0时,f(x)<0在x ![]() [1,2]上恒成立,求实数a的取值范围.
[1,2]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
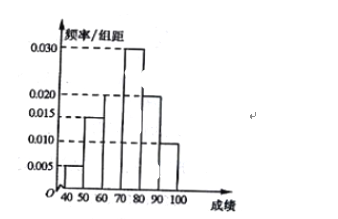
【题目】某中学举行了数学测试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.
(I)若该所中学共有3000名学生,试利用样本估计全校这次考试中优秀生人数;
(II)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人,试求恰好抽中1名优秀生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为
的右焦点为 ![]() ,且点
,且点 ![]() 在椭圆
在椭圆 ![]() 上.
上.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过椭圆 ![]() 上异于其顶点的任意一点
上异于其顶点的任意一点 ![]() 作圆
作圆 ![]() 的两条切线,切点分别为
的两条切线,切点分别为 ![]() (
( ![]() 不在坐标轴上),若直线
不在坐标轴上),若直线 ![]() 在
在 ![]() 轴,
轴, ![]() 轴上的截距分别为
轴上的截距分别为 ![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com