
已知椭圆 (a>b>0)经过点M(
(a>b>0)经过点M( ,1),离心率为
,1),离心率为 .
.
(1)求椭圆的标准方程;
(2)已知点P( ,0),若A,B为已知椭圆上两动点,且满足
,0),若A,B为已知椭圆上两动点,且满足 ,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
(1)  (2) 直线
(2) 直线 经过定点
经过定点
解析试题分析:(1) 椭圆 (a>b>0)经过点M(
(a>b>0)经过点M( ,1)
,1) ,
,
且有 ,通过解方程可得
,通过解方程可得 从而得椭圆的标准方程.
从而得椭圆的标准方程.
(2) 设 当直线
当直线 与
与 轴不垂直时,设直线的方程为
轴不垂直时,设直线的方程为
由


另一方面:

通过以上两式就不难得到关于 的等式,从而探究直线
的等式,从而探究直线 是否过定点;
是否过定点;
至于直线AB斜率不存在的情况,只需对上面的定点进行检验即可.
试题解析:
解:(1)由题意得 ①
①
因为椭圆经过点 ,所以
,所以 ②
②
又 ③
③
由①②③解得
所以椭圆方程为 . 4分
. 4分
(2)解:①当直线 与
与 轴不垂直时,设直线的方程为
轴不垂直时,设直线的方程为
代入 ,消去
,消去 整理得
整理得 6分
6分
由 得
得 (*)
(*)
设 则
则
所以,
= 8分
8分
得

整理得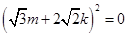
从而 且满足(*)
且满足(*)
所以直线 的方程为
的方程为 10分
10分
故直线 经过定点
经过定点 2分
2分
②当直线 与
与 轴垂直时,若直线为
轴垂直时,若直线为 ,此时点
,此时点 、
、 的坐标分别为
的坐标分别为  、
、 ,亦有
,亦有 12分
12分
综上,直线 经过定点
经过定点 . 13分
. 13分
考点:1、椭圆的标准方程;2、向量的数量积;3、直线与椭圆的位置关系.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com