
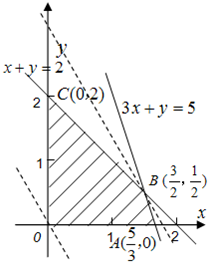
 解:设该农民种x亩水稻,y亩花生时,能获得利润z元.
解:设该农民种x亩水稻,y亩花生时,能获得利润z元.| 16 |
| 7 |
| z |
| 420 |
|
|
| 16 |
| 7 |
| 16 |
| 7 |
| z |
| 420 |
| z |
| 420 |
|
| 3 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年广东湛江市第二中学高一下学期期末考试数学卷 题型:解答题
(本小题满分14分)
一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤。但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元。现该农民手头有400元,两种作物各种多少,才能获得最大收益?
查看答案和解析>>
科目:高中数学 来源:2013届度广东省山一高二数学期文科数学试卷 题型:解答题
一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤。但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元。现该农民手头有400元;(1)设该农民种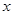 亩水稻,
亩水稻, 亩花生,利润
亩花生,利润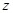 元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?
元,请写出约束条件及目标函数;(2)问两种作物各种多少,才能获得最大收益?
查看答案和解析>>
科目:高中数学 来源:2010年广东湛江市高一下学期期末考试数学卷 题型:解答题
(本小题满分14分)
一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤。但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元。现该农民手头有400元,两种作物各种多少,才能获得最大收益?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com