
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)![]()
![]() ;(2)
;(2)![]() .
.
【解析】
(1)设出点P的坐标,向量坐标化得到![]() 的表达式,进而得到最值;(2)
的表达式,进而得到最值;(2)![]() 为锐角即
为锐角即![]() ,设出点AB的坐标,向量坐标化得到点积的表达式为:x1x2+y1y2,联立直线和椭圆方程,由韦达定理得到结果.
,设出点AB的坐标,向量坐标化得到点积的表达式为:x1x2+y1y2,联立直线和椭圆方程,由韦达定理得到结果.
(1)由已知得,F1(-![]() ,0),F2(
,0),F2(![]() ,0),设点P(x,y),
,0),设点P(x,y),
则![]() +y2=1,且-2≤x≤2.
+y2=1,且-2≤x≤2.
所以![]() ·
·![]() =(-
=(-![]() -x,-y)·(
-x,-y)·(![]() -x,-y)=x2-3+y2=x2-3+1-
-x,-y)=x2-3+y2=x2-3+1-![]() =
=![]() x2-2,
x2-2,
当x=0,即P(0,±1)时,(![]() ·
·![]() )min=-2;
)min=-2;
当x=±2,即P(±2,0)时,(![]() ·
·![]() )max=1.
)max=1.
(2)由题意可知,过点M(0,2)的直线l的斜率存在.
设l的方程为y=kx+2,
由 消去y,化简整理得
消去y,化简整理得
(1+4k2)x2+16kx+12=0,Δ=(16k)2-48(1+4k2)>0,解得k2>![]() .
.
设A(x1,y1),B(x2,y2),则x1+x2=-![]() ,x1x2=
,x1x2=![]() ,
,
又∠AOB为锐角,所以![]() ·
·![]() >0,即x1x2+y1y2>0,
>0,即x1x2+y1y2>0,
有x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4
=(1+k2)·![]() +2k·
+2k·![]() +4>0,解得k2<4,
+4>0,解得k2<4,
所以![]() <k2<4,即k∈
<k2<4,即k∈![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线C关于
中,抛物线C关于![]() 轴对称,顶点为坐标原点,且经过点
轴对称,顶点为坐标原点,且经过点![]() .
.
(1)求抛物线C的标准方程;
(2) 过点![]() 的直线交抛物线于M、N两点.是否存在定直线
的直线交抛物线于M、N两点.是否存在定直线![]() ,使得l上任意点P与点M,Q,N所成直线的斜率
,使得l上任意点P与点M,Q,N所成直线的斜率![]() ,
,![]() ,
,![]() 成等差数列.若存在,求出直线l的方程;若不存在,说明理由.
成等差数列.若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数![]() ,
,![]() (0,
(0,![]() )为
)为![]() 型函数,共中
型函数,共中![]() .
.
(1)若![]() 是
是![]() 型函数,求函数
型函数,求函数![]() 的值域;
的值域;
(2)若![]() 是
是![]() 型函数,求函数
型函数,求函数![]() 极值点个数;
极值点个数;
(3)若![]() 是
是![]() 型函数,在
型函数,在![]() 上有三点A、B、C横坐标分別为
上有三点A、B、C横坐标分別为![]() 、
、![]() 、
、![]() ,其中
,其中![]() <
<![]() <
<![]() ,试判断直线AB的斜率与直线BC的斜率的大小并说明理由.
,试判断直线AB的斜率与直线BC的斜率的大小并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
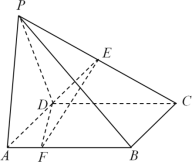
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)设二面角![]() 的平面角为
的平面角为![]() ,试判断在线段
,试判断在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占![]() ,三星销量约占
,三星销量约占![]() ,苹果销量约占
,苹果销量约占![]() ),根据该图,以下结论中一定正确的是( )
),根据该图,以下结论中一定正确的是( )
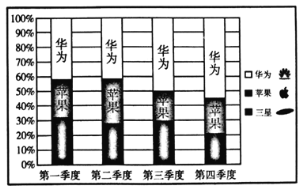
A. 四个季度中,每季度三星和苹果总销量之和均不低于华为的销量
B. 苹果第二季度的销量小于第三季度的销量
C. 第一季度销量最大的为三星,销量最小的为苹果
D. 华为的全年销量最大
查看答案和解析>>
科目:高中数学 来源: 题型:
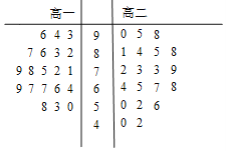
【题目】某学校为了解学生的体质健康状况,对高一、高二两个年级的学生进行了体质测试.现从两个年级学生中各随机选取20人,将他们的测试数据,用茎叶图表示如图:《国家学生体质健康标准》的等级标准如表.规定:测试数据≥60,体质健康为合格.
等级 | 优秀 | 良好 | 及格 | 不及格 |
测试数据 |
|
|
|
|
(Ⅰ)从该校高二年级学生中随机选取一名学生,试估计这名学生体质健康合格的概率;
(Ⅱ)从两个年级等级为优秀的样本中各随机选取一名学生,求选取的两名学生的测试数据平均数大于95的概率;
(Ⅲ)设该校高一学生测试数据的平均数和方差分别为![]() ,高二学生测试数据的平均数和方差分别为
,高二学生测试数据的平均数和方差分别为![]() ,试估计
,试估计![]() 、
、![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与x轴平行,求a的值;
处的切线与x轴平行,求a的值;
(Ⅱ)若![]() 在
在![]() 处取得极大值,求a的取值范围;
处取得极大值,求a的取值范围;
(Ⅲ)当a=2时,若函数![]() 有3个零点,求m的取值范围.(只需写出结论)
有3个零点,求m的取值范围.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点F为抛物线![]() 的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为
的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为![]() 时,
时,![]() .
.
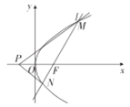
(1)求抛物线C的方程.
(2)点![]() ,证明:直线PM,PN关于x轴对称.
,证明:直线PM,PN关于x轴对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com