【题目】湖北省2019年公布了新的高考方案，实行“3+1+2”模式.某学生按方案要求任意选择，则该生选择考历史和化学的概率为_______.
【答案】
【解析】
根据题意，利用列举法列出一名学生在“3+1+2”中对“1+2”选择的所有可能情况，再列举出选择考历史和化学的情况，最后根据古典概型求出该生选择考历史和化学的概率.
解：根据新的高考方案，可知“3+1+2”模式中，
“3”是高考中必考的三门科目：语文、数学、外语，
“1”是必须在物理和历史中选择一门，
“2”是在化学、地理、思想政治、生物中选择2门，
对于任意一名学生，其在“3+1+2”中对“1+2”选择，所有可能情况如下：
①物理，生物，化学；②物理，生物，地理；③物理，生物，政治；
④物理，化学，地理；⑤物理，化学，政治；⑥物理，地理，政治；
⑦历史，生物，化学；⑧历史，生物，地理；⑨历史，生物，政治；
⑩历史，化学，地理；历史，化学，政治；历史，地理，政治；
共12种不同选择方法，
其中选择考历史和化学有以下情况：
①历史，生物，化学；②历史，化学，地理；③历史，化学，政治，
共3中不同的选择，
则在所有选项中某学生选择考历史和化学的概率为：
.
故答案为：.
科目：高中数学 来源： 题型：
【题目】某钢铁加工厂新生产一批钢管，为了了解这批产品的质量状况，检验员随机抽取了
件钢管作为样本进行检测，将它们的内径尺寸作为质量指标值，由检测结果得如下频率分布表和频率分布直方图：
分组 | 频数 | 频率 |
|
|
|
| ||
|
| |
| ||
| ||
|
|
|
|
|
|
合计 |
|
|
（1）求
，
；
（2）根据质量标准规定：钢管内径尺寸大于等于
或小于
为不合格，钢管内径尺寸在
或
为合格，钢管内径尺寸在
为优等.钢管的检测费用为
元/根，把样本的频率分布作为这批钢管的概率分布.
（i）若从这批钢管中随机抽取
根，求内径尺寸为优等钢管根数
的分布列和数学期望；
（ii）已知这批钢管共有
根，若有两种销售方案：
第一种方案：不再对该批剩余钢管进行检测，扣除根样品中的不合格钢管后，其余所有钢管均以
元/根售出；
第二种方案：对该批钢管进行一一检测，不合格钢管不销售，并且每根不合格钢管损失
元，合格等级的钢管元/根，优等钢管
元/根.
请你为该企业选择最好的销售方案，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角梯形
中，
，
，
，
，
，
为线段
（含端点）上的一个动点.设
，
，对于函数
，下列描述正确的是（ ）
A.
的最大值和
无关B.的最小值和无关
C.的值域和无关D.在其定义域上的单调性和无关
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）若
，求曲线
在点
处的切线方程；
（2）若函数
在其定义域内为增函数，求
的取值范围；
（3）在（2）的条件下，设函数
，若在
上至少存在一点
，使得
成立，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平面内两点M（4，﹣2），N（2，4）．
（1）求MN的垂直平分线方程；
（2）直线l经过点A（3，0），且与直线MN平行，求直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数
、
，给定下列命题：（1）不等式
的解集为
；（2）函数
在
上单调递增，在
上单调递减；（3）若函数
有两个极值点，则
；（4）若
时，总有
恒成立，则
1.其中正确命题的序号为_________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查，张三提供了该县某山羊养殖场年养殖数量
（单位：万只）与相应年份
（序号）的数据表和散点图（如图所示），根据散点图，发现与有较强的线性相关关系，李四提供了该县山羊养殖场的个数
（单位：个）关于的回归方程
.
年份序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年养殖山羊y/万只 | 1.2 | 1.5 | 1.6 | 1.6 | 1.8 | 2.5 | 25 | 2.6 | 2.7 |
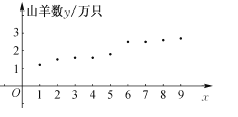
根据表中的数据和所给统计量，求关于
的线性回归方程（参考统计量：
，
）；
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为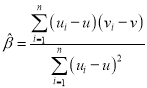
，
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
