
【题目】已知函数 ![]() ,在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
,在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形. 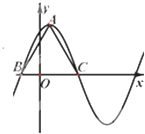
(Ⅰ)求ω的值及函数f(x)的值域;
(Ⅱ)若x∈[0,1],求函数f(x)的值域;
(Ⅲ)若 ![]() ,且
,且 ![]() ,求f(x0+1)的值.
,求f(x0+1)的值.
【答案】解:(Ⅰ)由已知可得:f(x)=6 ![]() +
+ ![]() sinωx﹣3(ω>0) =3cosωx+
sinωx﹣3(ω>0) =3cosωx+ ![]() sinωx
sinωx
=2 ![]() sin(ωx+
sin(ωx+ ![]() ),
),
又由于正△ABC的高为2 ![]() ,则BC=4,
,则BC=4,
∴函数f(x)的周期T=4×2=8,即 ![]() =8,
=8,
∴ω= ![]()
∴函数的值域为[﹣2 ![]() ,2
,2 ![]() ]
]
(Ⅱ)∵0≤x≤1,
∴ ![]() ≤
≤ ![]() x+
x+ ![]() ≤
≤ ![]() +
+ ![]() ,
,![]() ≤sin(
≤sin( ![]() x+
x+ ![]() )≤1,
)≤1,
3≤2 ![]() sin(
sin( ![]() +
+ ![]() )≤2
)≤2 ![]()
∴函数f(x)的值域为[3,2 ![]() ]
]
(Ⅲ)因为f(x0)= ![]() 由(Ⅰ)有f(x0)=2
由(Ⅰ)有f(x0)=2 ![]() sin(
sin( ![]() +
+ ![]() )=
)= ![]() ,即sin(
,即sin( ![]() +
+ ![]() )=
)= ![]() ,
,
由x0∈(﹣ ![]() ,
, ![]() )得:(
)得:( ![]() +
+ ![]()
![]() )∈(﹣
)∈(﹣ ![]() ,
, ![]() ),
),
所以,cos( ![]() +
+ ![]() )=
)= 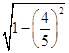 =
= ![]()
故f(x0+1)=2 ![]() sin(
sin( ![]() +
+ ![]() +
+ ![]() )=2
)=2 ![]() sin[(
sin[( ![]() +
+ ![]() )+
)+ ![]() ]=2
]=2 ![]() sin[(
sin[( ![]() +
+ ![]() )cos
)cos ![]() +cos(
+cos( ![]() +
+ ![]() )sin
)sin ![]()
=2 ![]() (
( ![]() ×
× ![]() +
+ ![]() ×
× ![]() )=
)= ![]()
【解析】(Ⅰ)将f(x)化简为f(x)=2 ![]() sin(ωx+
sin(ωx+ ![]() ),由正三角形△ABC的高为2
),由正三角形△ABC的高为2 ![]() 可求得BC,从而可求得其周期,继而可得ω 及函数f(x)的值域;(Ⅱ)由0≤x≤1,可求得
可求得BC,从而可求得其周期,继而可得ω 及函数f(x)的值域;(Ⅱ)由0≤x≤1,可求得 ![]() x+
x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],利用正弦函数的性质可求得函数f(x)的值域;(Ⅲ)由x0∈(﹣
],利用正弦函数的性质可求得函数f(x)的值域;(Ⅲ)由x0∈(﹣ ![]() ,
, ![]() )可求得(
)可求得( ![]() +
+ ![]() )∈(﹣
)∈(﹣ ![]() ,
, ![]() ),从而可求得cos(
),从而可求得cos( ![]() +
+ ![]() ),最后利用两角和的正弦即可求得f(x0+1)的值.
),最后利用两角和的正弦即可求得f(x0+1)的值.
【考点精析】利用两角和与差的正弦公式和二倍角的余弦公式对题目进行判断即可得到答案,需要熟知两角和与差的正弦公式:![]() ;二倍角的余弦公式:
;二倍角的余弦公式:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+xlnx(a∈R)
(1)若函数f(x)在区间[e,+∞)上为增函数,求a的取值范围;
(2)当a=1且k∈Z时,不等式k(x﹣1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网理财平台为增加平台活跃度决定举行邀请好友拿奖励活动,规则是每邀请一位好友在该平台注册,并购买至少1万元的12月定期,邀请人可获得现金及红包奖励,现金奖励为被邀请人理财金额的![]() ,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
理财金额 |
|
|
|
乙理财相应金额的概率 |
|
|
|
丙理财相应金额的概率 |
|
|
|
(1)求乙、丙理财金额之和不少于5万元的概率;
(2)若甲获得奖励为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ae﹣x , 若f′(x)≥2 ![]() 恒成立,则a的取值范围为( )
恒成立,则a的取值范围为( )
A.[3,+∞)
B.(0,3]
C.[﹣3,0)
D.(﹣∞,﹣3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知a,b∈(0,+∞),求证:x,y∈R,有 ![]() ≥
≥ ![]() ;
;
(2)若0<a<2,0<b<2,0<c<2,求证:(2﹣a)b,(2﹣b)c,(2﹣c)a不能同时大于1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过定点P(2,0)的直线l与曲线y= ![]() 相交于A,B两点,O为坐标原点,当△AOB的面积取最大时,直线的倾斜角可以是:①30°;②45°;③60°;④120°⑤150°.其中正确答案的序号是 . (写出所有正确答案的序号)
相交于A,B两点,O为坐标原点,当△AOB的面积取最大时,直线的倾斜角可以是:①30°;②45°;③60°;④120°⑤150°.其中正确答案的序号是 . (写出所有正确答案的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若两条异面直线所成的角为90°,则称这对异面直线为“理想异面直线对”,在连接正方体各顶点的所有直线中,“理想异面直线对”的对数为( )
A.24
B.48
C.72
D.78
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com