【题目】古希腊亚历山大时期的数学家帕普斯（Pappus，约300～约350）在《数学汇编》第3卷中记载着一个定理：“如果同一平面内的一个闭合图形的内部与一条直线不相交，那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以重心旋转所得周长的积.”如图，半圆
的直径
，点
是该半圆弧的中点，半圆弧与直径
所围成的半圆面（阴影部分不含边界）的重心
位于对称轴
上.若半圆面绕直径所在直线旋转一周，则所得到的旋转体的体积为__________
,
___________________
．
科目：高中数学 来源： 题型：
【题目】据市场调查发现，某种产品在投放市场的30天中，其销售价格
（元）和时间
（天）的关系如图所示．
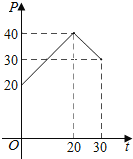
（1）求销售价格（元）和时间
（天）的函数关系式；
（2）若日销售量
（件）与时间（天）的函数关系式是
,问该产品投放市场第几天时，日销售额
（元）最高，且最高为多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|x+a|+|x﹣2|
（1）当a=﹣3时，求不等式f（x）≥3的解集；
（2）若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某商品的进货单价为1元/件，商户甲往年以单价2元/件销售该商品时，年销量为1万件.今年拟下调销售单价以提高销量增加收益.据估算，若今年的实际销售单价为
元/件
，则新增的年销量
（万件）.
（Ⅰ）写出今年商户甲的收益
（单位：万元）与的函数关系式；
（Ⅱ）商户甲今年采取降低单价提高销量的营销策略，是否能获得比往年更大的收益（即比往年收益更多）？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂生产不同规格的一种产品，根据检测标准，其合格产品的质量
与尺寸
之间满足关系式
（
为大于0的常数），现随机抽取6件合格产品，测得数据如下：
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
（1）求
关于
的回归方程；（提示：
与
有线性相关关系）
（2）按照某项指标测定，当产品质量与尺寸的比在区间
内时为优等品，现从抽取的6件合格产品再任选3件，求恰好取得两件优等品的概率.
参考数据及公式：
，
，
，
对于样本
（
），其回归直线
的斜率和截距的最小二乘估计公式分别为：
，
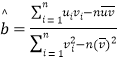查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
=1，（a＞b＞0）的离心率为 
，以原点为圆心，椭圆的短半轴长为半径的圆与直线x﹣y+ 
=0）且不垂直于x轴直线l椭圆C相交于A、B两点． （Ⅰ）求椭圆C的方程；
（Ⅱ）求 
取值范围；
（Ⅲ）若B关于x轴的对称点是E，证明：直线AE与x轴相交于定点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中心均在原点的椭圆与双曲线有公共焦点，且左、右焦点分别为F1、F2 ， 这两条曲线在第一象限的交点为P，△PF1F2是以PF1为底边的等腰三角形．若|PF1|=10，椭圆与双曲线的离心率分别为e1、e2 ， 则e1e2的取值范围为（ ）
A.
B.
C.（2，+∞）
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种蔬菜从1月1日起开始上市，通过市场调查，得到该蔬菜种植成本
（单位：元/
）与上市时间
（单位：10天）的数据如下表：
时间 | 5 | 11 | 25 |
种植成本 | 15 | 10.8 | 15 |
（1）根据上表数据，从下列函数：
，
，
，
中（其中
），选取一个合适的函数模型描述该蔬菜种植成本与上市时间的变化关系；
（2）利用你选取的函数模型，求该蔬菜种植成本最低时的上市时间及最低种植成本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
