
����Ŀ������˵����ȷ���ǣ� ��
A. ij��һ����Ʒ�Ĵ�Ʒ��Ϊ![]() ���������ȡ����10����Ʒһ���ᷢ��һ����Ʒ
���������ȡ����10����Ʒһ���ᷢ��һ����Ʒ
B. ��һöӲ�ң���������5���������ϣ������γ��ַ������ϵĸ������������ϵĸ�����Ȼ��Ϊ0.5
C. ijҽԺ����һ�ּ�����������Ϊ10%����ôǰ9�����˶�û����������10���˾�һ��������
D. ������Ԥ����������ĸ�����90%��˵������õ���90%�ĵط�Ҫ���꣬����10%�ĵط���������
���𰸡�B
����������������������¼���Ƶ�ʵĸ�����¼����ʵĺ����ж����ɣ�
��⣺
A.��Ʒ�Ĵ�Ʒ����ͨ�������IJ�Ʒͨ��ʵ��õ������ݣ���Ŀ�еIJ�Ʒ�������٣��ʲ���ȷ��
B.��Ӳ��������泯�ϵĸ�����ͨ������ʵ��õ���ȷ��ֵ����ʵ������أ�����ȷ��
C.����ͬAѡ�Ҳ����ȷ��
D���¼��ĸ����Ǵ���ʵ���õ��Ľ������ȷ��ֵ����ʵ������أ�����Dѡ���˵�����ֵIJ��Ǹ��ʵĸ���ʲ���ȷ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ ������
������![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ����ļ�����ϵ�У���
���������Ϊ����ļ�����ϵ�У���![]() �ļ�����Ϊ
�ļ�����Ϊ![]() �� ֱ��
�� ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1����ֱ��![]() ��ֱ�����귽��������
��ֱ�����귽��������![]() ����ͨ���̣�
����ͨ���̣�
��2����![]() ������
������![]() �ϵĶ��㣬
�ϵĶ��㣬 ![]() Ϊ�߶�
Ϊ�߶�![]() ���е�.���
���е�.���![]() ��ֱ��
��ֱ��![]() �ľ�������ֵ.
�ľ�������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ó��Ħ������.�ر����������ҹ���Ϊ������.���������Ի�Ϊ�����������ٰ���ѣ������ϼӴ�Ը�����ʩѹ����£���ǵ��ƻ�Ϊ5G��Ȼ���Ⲣû���û�Ϊȴ��.��Ϊ��2018�겻���������¼�¼����������ͬ��ǿ��.���꣬�ҹ���Ϊijһ��ҵΪ�˽�һ�������г����������ƻ���2020�������¼�������ij�����ֻ�.ͨ���г������������˿��ֻ�ȫ����Ͷ��̶��ɱ�250��ÿ����![]() ��ǧ�����ֻ�������Ͷ��ɱ�
��ǧ�����ֻ�������Ͷ��ɱ�![]() ��Ԫ����
��Ԫ����  �����г�����֪��ÿ���ֻ��ۼ�0.7��Ԫ����ȫ�����������ֻ�������ȫ��������.
�����г�����֪��ÿ���ֻ��ۼ�0.7��Ԫ����ȫ�����������ֻ�������ȫ��������.
��![]() �����2020�������
�����2020�������![]() ����Ԫ�����������
����Ԫ�����������![]() ��ǧ�����ĺ�����ϵʽ��������=���۶�ɱ�����
��ǧ�����ĺ�����ϵʽ��������=���۶�ɱ�����
![]() 2020�����Ϊ���٣�ǧ����ʱ����ҵ�������������������Ƕ��٣�
2020�����Ϊ���٣�ǧ����ʱ����ҵ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���о����֣����� PM 2.5 ����Ҫ��Դ����������ȼú��������ȼ�ա�����β�����������ա���ҵ��Ⱦ�Ͷ��������ܽ�������ȼú��ƽ������ռ��ԼΪ 18%��Ϊʵ�֡����ܼ��š���������ˮ���족�����������С�ú�ĵ硱���̣����ÿ���Դ�ȱ���Ϊ���칩ů�����붬�����������о����õ��������ӣ�Ϊ��֤����ȡů���й��粿�ŶԸ��� 100 ���������� 120 ����㣩ȡů�õ�������λ���ȣ�����ͳ�Ʒ������õ�����ȡů�õ�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��

��1����Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2������ 100 �������������ȡ 1 ��������ȵ��飬���⻧����ȡů�õ�����[3300,3400]�ĸ��ʣ�
��3�����õ���Ϊ[3200,3250)��[3250,3300)��[3300,3350)��[3350,3400]����������У��÷ֲ�����ķ�����ȡ 34 ��������е��飬��Ӧ���õ�����[3200,3250)�ľ����г�ȡ���ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����x��R������f��x��=f��2-x�����Ҷ������x1��x2�ʣ�-�ޣ�1]��x1��x2���У�x1-x2����f��x1��-f��x2������0��������
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����������ı����Ϊ25�У�������������ͼ��ͼ��ʾ��������ͼ������������ֱ�������Σ��������ͼ��������ֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABCD�У�PA��ƽ��ABCD������ABCD��ֱ�����Σ�����AD��BC��AB��AD��AB=AD= ![]() BC��
BC�� ![]() =
= ![]()
![]() ��
�� 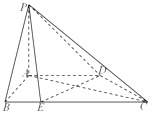
��1����֤��DE��ƽ��PAC��
��2����ֱ��PE��ƽ��PAC���ɽǵ�����ֵΪ ![]() ��������A��PC��D��ƽ��ǵ�����ֵ��
��������A��PC��D��ƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����C�� ![]() ��a��0��b��0�������ҽ���ֱ�ΪF1 �� F2 �� ��M��˫����C�Ľ��㲻�غϣ���M����F1 �� F2�ĶԳƵ�ֱ�ΪA��B���߶�MN���е���˫���ߵ���֧�ϣ���|AN|��|BN|=12����a=�� ��
��a��0��b��0�������ҽ���ֱ�ΪF1 �� F2 �� ��M��˫����C�Ľ��㲻�غϣ���M����F1 �� F2�ĶԳƵ�ֱ�ΪA��B���߶�MN���е���˫���ߵ���֧�ϣ���|AN|��|BN|=12����a=�� ��
A.3
B.4
C.5
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ������a��R����
������a��R����
��1�����ۺ���f��x������ż�ԣ���˵�����ɣ�
��2����![]() �����жϺ���f��x��������[1��+�ޣ��ϵĵ����ԣ����ú��������Զ������֤����
�����жϺ���f��x��������[1��+�ޣ��ϵĵ����ԣ����ú��������Զ������֤����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com