
【题目】已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)已知函数![]() ,利用上述性质,求函数
,利用上述性质,求函数![]() 的单调区间和值域;
的单调区间和值域;
(2)已知函数![]() =
=![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() (x2)=
(x2)=![]() 成立,求实数
成立,求实数![]() 的值.
的值.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且直线
,且直线![]() 恰好平分
恰好平分![]() .
.

(1)求![]() 的值;
的值;
(2)设![]() 是直线
是直线![]() 上一点,直线
上一点,直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某池塘里浮萍的面积![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:月)的关系为
(单位:月)的关系为![]() .关于下列说法正确的是( )
.关于下列说法正确的是( )
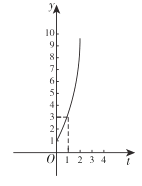
A.浮萍每月的增长率为![]()
B.浮萍每月增加的面积都相等
C.第![]() 个月时,浮萍面积不超过
个月时,浮萍面积不超过![]()
D.若浮萍蔓延到![]() 、
、![]() 、
、![]() 所经过的时间分别是
所经过的时间分别是![]() 、
、![]() 、
、![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月智能共享单车项目正式登陆某市,两种车型![]() “小绿车”、“小黄车”
“小绿车”、“小黄车”![]() 采用分时段计费的方式,“小绿车”每30分钟收费
采用分时段计费的方式,“小绿车”每30分钟收费![]() 元
元![]() 不足30分钟的部分按30分钟计算
不足30分钟的部分按30分钟计算![]() ;“小黄车”每30分钟收费1元
;“小黄车”每30分钟收费1元![]() 不足30分钟的部分按30分钟计算
不足30分钟的部分按30分钟计算![]() 有甲、乙、丙三人相互独立的到租车点租车骑行
有甲、乙、丙三人相互独立的到租车点租车骑行![]() 各租一车一次
各租一车一次![]() 设甲、乙、丙不超过30分钟还车的概率分别为
设甲、乙、丙不超过30分钟还车的概率分别为![]() ,
,![]() ,
,![]() ,三人租车时间都不会超过60分钟
,三人租车时间都不会超过60分钟![]() 甲、乙均租用“小绿车”,丙租用“小黄车”.
甲、乙均租用“小绿车”,丙租用“小黄车”.
![]() 求甲、乙两人所付的费用之和等于丙所付的费用的概率;
求甲、乙两人所付的费用之和等于丙所付的费用的概率;
![]() 2
2![]() 设甲、乙、丙三人所付的费用之和为随机变量
设甲、乙、丙三人所付的费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,太阳能技术运用的步伐日益加快.2002年全球太阳能电池的年生产量达到670 MW,年生产量的增长率为34%.以后四年中,年生产量的增长率逐年递增2%(如,2003年的年生产量的增长率为36%).
(1)求2006年全球太阳能电池的年生产量(结果精确到0.1 MW);
(2)目前太阳能电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420MW.假设以后若干年内太阳能电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳能电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com