
【题目】[选修4-5:不等式选讲](10分)
已知函数f(x)=2|x-2|+3|x+3|.
(Ⅰ)解不等式:f(x)>15;
(Ⅱ)若函数f(x)的最小值为m,正实数a,b满足4a+25b=m,求![]() +
+![]() 的最小值,并求出此时a,b的大小.
的最小值,并求出此时a,b的大小.
【答案】(1) (-∞,-4)∪(2,+∞) (2) ![]()
【解析】试题分析:(1)通过讨论x的范围,求出不等式的解集即可;
(2)求出f(x)的最小值m,得到4a+25b=10,利用均值不等式求出![]() +
+![]() 的最小值.
的最小值.
试题解析:
(Ⅰ)依题意,2|x-2|+3|x+3|>15;
当x<-3时,原式化为2(2-x)-3(x+3)>15,解得x<-4;
当-3≤x≤2时,原式化为2(2-x)+3(x+3)>15,解得x>2,故不等式无解;
当x>2时,原式化为2(x-2)+3(x+3)>15,解得x>2;
综上所述,不等式的解集为(-∞,-4)∪(2,+∞).
(Ⅱ)由(Ⅰ)可知,当x=-3时,函数f(x)有最小值10,故4a+25b=10,
故![]() +
+![]() =
=![]()
![]() (4a+25b)=
(4a+25b)=![]()
![]() ≥
≥![]() ,
,
当且仅当![]() =
=![]() 时等号成立,此时a=,b=.
时等号成立,此时a=,b=.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为
的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,若点
,若点![]() 总在以线段
总在以线段![]() 为直径的圆内,求
为直径的圆内,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张A4纸的长宽之比为![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.现分别将△
的中点.现分别将△![]() ,△
,△![]() 沿
沿![]() ,
, ![]() 折起,且
折起,且![]() ,
, ![]() 在平面
在平面![]() 同侧,下列命题正确的是__________.(写出所有正确命题的序号)
同侧,下列命题正确的是__________.(写出所有正确命题的序号)

①![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点共面;
四点共面;
②当平面![]() 平面
平面![]() 时,
时, ![]() 平面
平面![]() ;
;
③当![]() ,
, ![]() 重合于点
重合于点![]() 时,平面
时,平面![]() 平面
平面![]() ;
;
④当![]() ,
, ![]() 重合于点
重合于点![]() 时,设平面
时,设平面![]() 平面
平面![]()
![]() ,则
,则![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
(1)求椭圆C的标准方程;
(2)设A,B,P为椭圆C上三点,满足![]() ,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
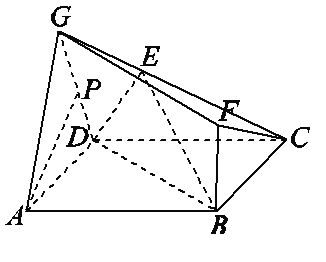
【题目】如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,BF⊥平面ABCD,∠GDC=90°,点E是线段GC上除两端点外的一点,若点P为线段GD的中点.
(Ⅰ)求证:AP⊥平面GCD;
(Ⅱ)求证:平面ADG∥平面FBC;
(Ⅲ)若AP∥平面BDE,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)(x∈D),若x∈D时,均有f′(x)<f(x)成立,则称函数f(x)是J函数.
(Ⅰ)当函数f(x)=x2+m(ex+x),x≥e是J函数时,求实数m的取值范围;
(Ⅱ)若函数g(x)为R+上的J函数,试比较g(a)与ea-1g(1)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点
经过点 ,离心率为
,离心率为![]() .
.
(1)求椭圆E的标准方程;
(2)若A1,A2分别是椭圆E的左、右顶点,过点A2作直线l与x轴垂直,点P是椭圆E上的任意一点(不同于椭圆E的四个顶点),连接PA1交直线l于点B,点Q为线段A2B的中点,求证:直线PQ与椭圆E只有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,,AC=AD=CD,E是AD的中点.
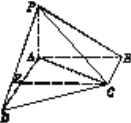
(Ⅰ)证明CE∥平面PAB;
(Ⅱ)证明:平面PAD⊥平面PCE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856261)
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(Ⅰ)下表是年龄的频率分布表,求正整数a,b的值;

(Ⅱ)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组抽取的员工的人数分别是多少?
(Ⅲ)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com