
| AЃЎ | 2 | BЃЎ | 3 | CЃЎ | 4 | DЃЎ | 5 |
ЗжЮі ЃЈ1ЃЉy=tanxдкЃЈkІа$\frac{Іа}{2}$ЃЌkІа+$\frac{Іа}{2}$ЃЉЪЧдіКЏЪ§
ЃЈ2ЃЉЃЌЁп-x2+2xЁм1Ёрy=2${\;}^{-{x}^{2}+2x}$Ём21ЃЌжЕгђЮЊЃЈ0ЃЌ2]ЃЎ
ЃЈ3ЃЉЃЌШєy=fЃЈ2xЃЉЕФЖЈвхгђЮЊ[1ЃЌ2]⇒2Ём2xЁм4ЃЌ2Ёмx-1Ём4ЃЌдђy=fЃЈx-1ЃЉЕФЖЈвхгђЮЊ[3ЃЌ5]ЃЎ
ЃЈ4ЃЉЃЌЁпM={ЃЈxЃЌyЃЉ|$\frac{y-3}{x-2}$=1}={ЃЈxЃЌyЃЉ|y-3=x-2ЃЌxЁй2}ЃЌдђЃЈ∁UMЃЉЁЩN={ЃЈ2ЃЌ3ЃЉ}ЃЎ
ЃЈ5ЃЉЃЌЛГіЭМЯѓМДПЩХаЖЯЃЛ
ЃЈ6ЃЉЃЌКЏЪ§y=lgsinЃЈ$\frac{Іа}{3}$-2xЃЉЕФЕЅЕїЕндіЧјМфЮЊЃЈkІа+$\frac{2Іа}{3}$ЃЌkІа+$\frac{11Іа}{12}$ЃЉЃЌЃЈkЁЪZЃЉЃЎ
НтД№ НтЃКЖдгкЃЈ1ЃЉЃЌy=tanxдкЃЈkІа$\frac{Іа}{2}$ЃЌkІа+$\frac{Іа}{2}$ЃЉЪЧдіКЏЪ§ЃЌЙЪДэЃЌ
ЖдгкЃЈ2ЃЉЃЌЁп-x2+2xЁм1Ёрy=2${\;}^{-{x}^{2}+2x}$Ём21ЃЌжЕгђЮЊЃЈ0ЃЌ2]ЃЌЙЪДэЃЎ
ЖдгкЃЈ3ЃЉЃЌШєy=fЃЈ2xЃЉЕФЖЈвхгђЮЊ[1ЃЌ2]⇒2Ём2xЁм4ЃЌ2Ёмx-1Ём4ЃЌдђy=fЃЈx-1ЃЉЕФЖЈвхгђЮЊ[3ЃЌ5]ЃЌЙЪе§ШЗЃЎ
ЖдгкЃЈ4ЃЉЃЌЁпM={ЃЈxЃЌyЃЉ|$\frac{y-3}{x-2}$=1}={ЃЈxЃЌyЃЉ|y-3=x-2ЃЌxЁй2}ЃЌдђЃЈ∁UMЃЉЁЩN={ЃЈ2ЃЌ3ЃЉ}ЃЌе§ШЗЃЎ
ЖдгкЃЈ5ЃЉЃЌШчЭМЗНГЬ3sin$\frac{Іа}{2}x={log_{\frac{1}{2}}}$xга5ИіЪЕЪ§ИљЃЎЙЪДэ
ЖдгкЃЈ6ЃЉЃЌКЏЪ§y=lgsinЃЈ$\frac{Іа}{3}$-2xЃЉЕФЕЅЕїЕндіЧјМфЮЊЃЈkІа+$\frac{2Іа}{3}$ЃЌkІа+$\frac{11Іа}{12}$ЃЉЃЌЃЈkЁЪZЃЉЃЌЙЪДэЃЎ
ЙЪбЁЃКA
ЕуЦР БОЬтПМВщСЫУќЬтецМйЕФХаЖЯЃЌЪєгкЛљДЁЬтЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈ-ЁоЃЌ-3] | BЃЎ | [-3ЃЌ1] | CЃЎ | [1ЃЌ+ЁоЃЉЁШЃЈ-ЁоЃЌ-3] | DЃЎ | [1ЃЌ+ЁоЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
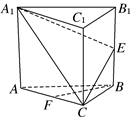 ШчЭМЃЌдке§Ш§РтжљABCA1B1C1жаЃЌEЃЌFЗжБ№ЮЊBB1ЃЌACЕФжаЕуЃЎЧѓжЄЃКBFЁЮЦНУцA1ECЃЎ
ШчЭМЃЌдке§Ш§РтжљABCA1B1C1жаЃЌEЃЌFЗжБ№ЮЊBB1ЃЌACЕФжаЕуЃЎЧѓжЄЃКBFЁЮЦНУцA1ECЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
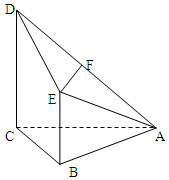 вбжЊЫФРтзЖA-BCDEЃЌЦфжаAB=BC=AC=BE=1ЃЌCD=2ЃЌCDЁЭУцABCЃЌBEЁЮCDЃЌFЮЊADЕФжаЕуЃЎ
вбжЊЫФРтзЖA-BCDEЃЌЦфжаAB=BC=AC=BE=1ЃЌCD=2ЃЌCDЁЭУцABCЃЌBEЁЮCDЃЌFЮЊADЕФжаЕуЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com