练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体ABCD﹣A1B1C1D1中，M，N，P分别是B1B，B1C1 ， CD的中点，则MN与D1P所成角的余弦值为（ ）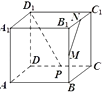

    A.
    B.
    C.
    D.

    【答案】B
    【解析】解：如图所示，建立空间直角坐标系．
    不妨设正方体的棱长AB=2．
    则D（0，0，0），P（0，1，0），D1（0，0，2），M（2，2，1），N（1，2，2）．
    ∴ ， ．
    ∴ = = =﹣ ．
    ∴MN与D1P所成角的余弦值为 ．
    故选B．

    【考点精析】根据题目的已知条件，利用异面直线及其所成的角的相关知识可以得到问题的答案，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD﹣A1B1C1D1中，

    （1）求证：AD1⊥平面CDA1B1；
    （2）求直线AD1与直线BD所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数），以原点为极点， 轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

    写出曲线的极坐标的方程以及曲线的直角坐标方程；

    若过点（极坐标）且倾斜角为的直线与曲线交于， 两点，弦的中点为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的圆锥中，OP是圆锥的高，AB是底面圆的直径，点C是弧AB的中点，E是线段AC的中点，D是线段PB的中点，且PO=2，OB=1．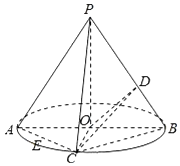

    （1）试在PB上确定一点F，使得EF∥面COD，并说明理由；
    （2）求点A到面COD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图， ， ， ， 是圆柱底面圆周的四等分点， 是圆心， ， ， 与底面垂直，底面圆的直径等于圆柱的高．

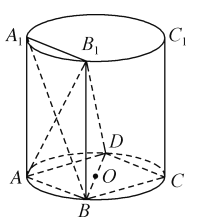
    （1）证明： ；

    （2）求二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有以下命题：
    ①如果向量 ， 与任何向量不能构成空间向量的一组基底，那么 ， 的关系是不共线；
    ②O，A，B，C为空间四点，且向量 ， ， 不构成空间的一个基底，则点O，A，B，C一定共面；
    ③已知向量 ， ， 是空间的一个基底，则向量 + ， ﹣ ， 也是空间的一个基底；
    ④△ABC中，A＞B的充要条件是sinA＞sinB．
    其中正确的命题个数是（ ）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列中， ，且对任意正整数都成立，数列的前项和为．

    （1）若，且，求；

    （2）是否存在实数，使数列是公比为1的等比数列，且任意相邻三项按某顺序排列后成等差数列，若存在，求出所有的值；若不存在，请说明理由；

    （3）若，求．（用表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】先后随机投掷2枚正方体骰子，其中x表示第1枚骰子出现的点数，y表示第2枚骰子出现的点数，
    （1）求点P（x，y）在直线y=x﹣1上的概率；
    （2）求点P（x，y）满足y2＜4x的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等差数列{an}中，已知an＞0，a1+a2+a3=15，且a1+2，a2+5，a3+13构成等比数列{bn}的前三项．
    （1）求数列{an}，{bn}的通项公式；
    （2）求数列{anbn}的前n项和Tn ．

    查看答案和解析>>

    同步练习册答案